
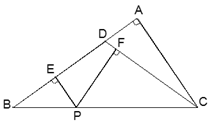
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
【答案】4![]()
【解析】结合已知AD:DB=1:4,BC=![]() ,应用勾股定理求出AC的长,连接PD,根据S△PBD+S△PCD=S△BCD,可得
,应用勾股定理求出AC的长,连接PD,根据S△PBD+S△PCD=S△BCD,可得![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() BDAC,继而得到PE+PF=AC即可得.
BDAC,继而得到PE+PF=AC即可得.
∵AD:DB=1:4,
∴设AD=n,BD=4n,
∴AB=5n,
∵DB=DC,∴DC=4n,
∵∠A=90°,∴AC2=DC2-AD2=15n2,AB2+AC2=BC2,
∵BC=4![]() ,
,
∴(5n)2+15n2=![]() ,
,
∴n2=![]() ,∴AC=
,∴AC=![]() =
=![]() ,
,
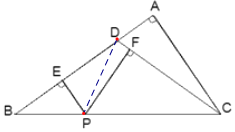
连接PD,PD把△BCD分成两个三角形△PBD,△PCD,
∵PE⊥AB ,PF⊥CD,AC⊥BD,
∴S△PBD=![]() BDPE,
BDPE,
S△PCD=![]() DCPF,
DCPF,
S△BCD=![]() BDAC,
BDAC,
∵S△PBD+S△PCD=S△BCD,
∴![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() BDAC,
BDAC,
∵DB=DC,
∴PE+PF=AC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.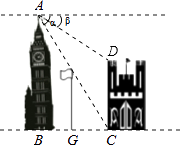
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市初中学生上学的交通方式,从中随机调查了a名学生的上学交通方式,统计结果如图. 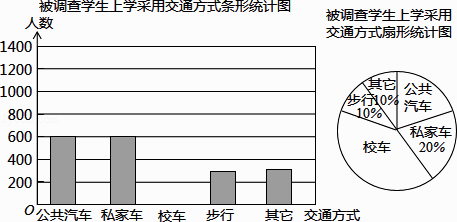
(1)求a的值;
(2)补全条形统计图并求出乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数;
(3)该市共有初中学生15000名,请估计其中坐校车上学的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知点A、点B是直线上的两点,AB =12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过 秒时线段PQ的长为5厘米.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,CD是AB边上的高,AC=8,∠ACD=30°,tan∠ACB=![]() ,点P为CD上一动点,当BP+
,点P为CD上一动点,当BP+![]() CP最小时,DP=_________.
CP最小时,DP=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
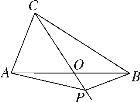
【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
查看答案和解析>>
科目:初中数学 来源: 题型:
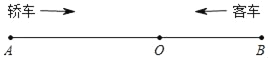
【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 , ∠CAC′=°.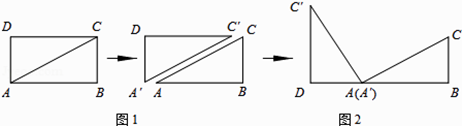
(2)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.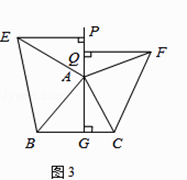
(3)如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,说明理由.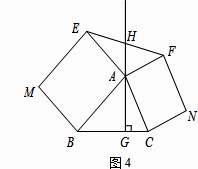
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com