
【题目】如图,ΔABC中,CD是AB边上的高,AC=8,∠ACD=30°,tan∠ACB=![]() ,点P为CD上一动点,当BP+
,点P为CD上一动点,当BP+![]() CP最小时,DP=_________.
CP最小时,DP=_________.

【答案】![]()
【解析】作 PE⊥AC 于 E,BE′⊥AC 于 E′ 交 CD 于 P′.
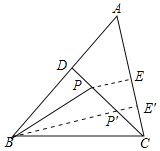
∵CD⊥AB,∠ACD=30°,∠PEC=90°,AC=8 ,
∴PE=![]() PC,∠A=60°,∠ABE′=30°,AD=4,CD=4
PC,∠A=60°,∠ABE′=30°,AD=4,CD=4![]() ,
,
∴PB+![]() PC=PB+PE ,
PC=PB+PE ,
∴ 当 BE′⊥AC 时 ,PB+PE=BP′+P′E′=BE′最小,
∵tan∠ACB=![]() =
=![]() ,设 BE′=5
,设 BE′=5![]() k,CE′=3k ,
k,CE′=3k ,
∴AE′=83k,AB=166k,BD=166k4=126k ,
∴BC2=BD2+CD2=BE′2+CE′2 ,
∴(126k)2+48=9k2+75k2 ,
整理得 k2+3k4=0 ,
∴k=1或4( 舍去 ) ,
∴BE′=5![]() ,CE′=3
,CE′=3
在Rt△CE′P′中,∠ACD=30°,CE′=3,可求得CP′=2![]() ,
,
∴DP′=CD-CP′=4![]() -2
-2![]() =2
=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
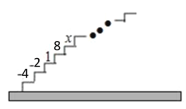
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣4,﹣2,1,8,且任意相邻四个台阶上数的和都相等.
尝试:(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用: 求从下到上39个台阶上数的和.
发现:试用含k(k为正整数)的代数式表示出数“1”所在的台阶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=kx+b的图象如图所示,则k,b的值可能为( )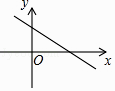
A.k=3,b=3
B.k=3,b=﹣3
C.k=﹣3,b=3
D.k=﹣3,b=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
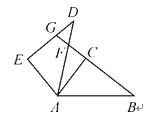
【题目】如图所示,△ABC≌△ADE,BC的延长线交AD于点F,交DE于点G,若∠CAD=20°,∠B=∠D=35°,∠EAB=120°,求∠AED,∠BFD以及∠DGB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
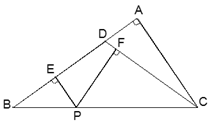
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,过AD的中点O作EF⊥AD,分别交AB、AC于点E、F,连接DE、DF. 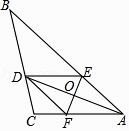
(1)判断四边形AFDE是什么四边形?请说明理由;
(2)若BD=8,CD=3,AE=4,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现.老师调查了全班50名学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组:A:0.5≤x<1,B:1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).
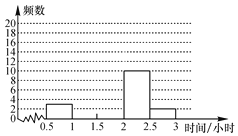
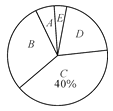
请根据图中提供的信息,解答下列问题:
(1)这次活动中学生做家务时间的中位数所在的组是____________;
(2)补全频数分布直方图;
(3)该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73, ![]() ≈1.7).
≈1.7).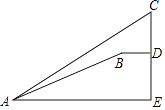
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com