
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.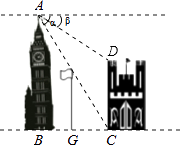
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π) 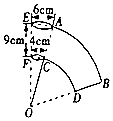
查看答案和解析>>
科目:初中数学 来源: 题型:
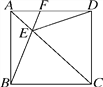
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若关于x的一元一次方程ax=b的解为b+a,则称该方程为“和解方程”. 例如:方程2x=﹣4的解为x=﹣2,而﹣2=﹣4+2,则方程2x=﹣4为“和解方程”.
请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程3x=m是“和解方程”,求m的值;
(2)已知关于x的一元一次方程﹣2x=mn+n是“和解方程”,并且它的解是x=n,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
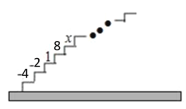
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣4,﹣2,1,8,且任意相邻四个台阶上数的和都相等.
尝试:(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用: 求从下到上39个台阶上数的和.
发现:试用含k(k为正整数)的代数式表示出数“1”所在的台阶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数轴上点A表示的数是8,点B表示的数是﹣4.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左运动.P,Q两点同时出发.
![]()
(1)经过多长时间,点P位于点Q左侧2个单位长度?
(2)在点P运动的过程中,若点M是AP的中点,点N是BP的中点,求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是( ) 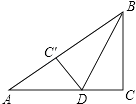
A.3cm2
B.4cm2
C.5cm2
D.6cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①相等的角是对顶角;②若![]() ,则
,则![]() 互补;③同一平面内的三条直线
互补;③同一平面内的三条直线![]() ,若
,若![]() 与
与![]() 相交,则
相交,则![]() 与
与![]() 相交;④在同一平面内,两条不重合的直线的位置关系可能是平行或垂直;⑤有公共顶点并且相等的角是对顶角.其中正确的有( )
相交;④在同一平面内,两条不重合的直线的位置关系可能是平行或垂直;⑤有公共顶点并且相等的角是对顶角.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
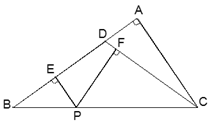
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com