
【题目】如图,直线y=4x与反比例函数y= ![]() (k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=
(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα= ![]() .
.
(1)求k的值.
(2)求点B的坐标.
(3)设点P点在y轴上,若△PAB是以AB为直角边的直角三角形,则点P的坐标为: .
【答案】
(1)解:把点A(1,a)代入y=4x中,得a=4,
所以A(1,4),
把点A(1,4)代入 ![]() 中,得k=4;
中,得k=4;
(2)解:过点B作BE垂直于x轴于点E,如图示,
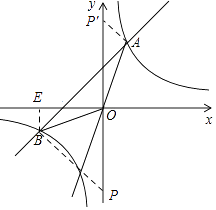
设BE长为m,在Rt△OBE中,
∵ ![]() ,
,
∴ ![]() ,即 OE=4BE=4m,
,即 OE=4BE=4m,
∴所以点B坐标为(﹣m,﹣4m),
把点B代入 ![]() 中,
中,
得:4m2=4,
解得m1=1,m2=﹣1(舍去)
∴点B坐标为(﹣4,﹣1);
(3)(0,5)或(0,﹣5)
【解析】解: (3)如图所示,过A作AP'⊥AB,交y轴于P',过B作BP⊥AB,交y轴于P,
根据A(1,4),B(﹣4,﹣1),可得直线AB的解析式为y=x+3;
根据直角坐标系中互相垂直的两直线的系数k互为负倒数,
可设直线BP为y=﹣x+m,
把B(﹣4,﹣1)代入可得,m=﹣5;
设直线AP'的解析式为y=﹣x+n,
把A(1,4)代入,可得n=5,
∴点P坐标为:(0,5),(0,﹣5).
所以答案是:(0,5)或(0,﹣5).
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中∠ABC=90°,AD平分∠BAC,点M、N分别是AD,AB上一动点,当AC=6时,BM+MN的最小值等于_______。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y= ![]() x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= ![]() 上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的 ![]() 的概率是 .
的概率是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某少年宫管、弦乐队共46人.其中管乐队人数少于23人,弦乐队人数不足45人,现准备
购买演出服装.下面是某服装厂给出的演出服装的价格
购买服装的套数 | 1套至23套 | 24套至44套 | 45套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果管乐队、弦乐队分别单独购买服装,一共需付2500元.
(1)管乐队、弦乐队各多少人?
(2)如果管乐队、弦乐队联合起来购买服装.那么比两队各自购买服装共可以节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,为减少交叉感染,催生了以智能技术为支撑的无接触服务.某快递公司准备购进![]() ,
,![]() 两种型号的智能机器人送快递.经市场调査发现,
两种型号的智能机器人送快递.经市场调査发现,![]() 型号机器人的单价比
型号机器人的单价比![]() 型号机器人贵600元,3台
型号机器人贵600元,3台![]() 型号机器人比2台
型号机器人比2台![]() 型号机器人贵1200元.
型号机器人贵1200元.
(1)求![]() ,
,![]() 两种型号机器人的单价各是多少元?
两种型号机器人的单价各是多少元?
(2)若该快递公司准备用不超过132000元购进![]() ,
,![]() 两种型号机器人共50台,请问该快递公司最多可购进
两种型号机器人共50台,请问该快递公司最多可购进![]() 型号机器人多少台?
型号机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弦BE与弦CD交于点G,点E为 ![]() 的中点,过点B的直线交DC延长线于点A,AB∥DE.
的中点,过点B的直线交DC延长线于点A,AB∥DE.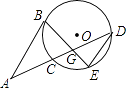
(1)若AB=AG,求证:AB是⊙O切线;
(2)在(1)条件下,若tanA= ![]() ,DE=10,求⊙O的半径.
,DE=10,求⊙O的半径.
(3)求证:AG2﹣BG2=ACAG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线
为直线![]() 上一点,
上一点,![]()


(1)如图1,当![]() 在
在![]() 上,
上,![]() 在
在![]() 上时,求证
上时,求证![]() ;
;
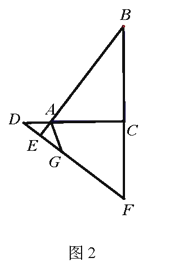
(2)如图2,当![]() 在
在![]() 的延长线上,
的延长线上,![]() 在
在![]() 的延长线上时,点
的延长线上时,点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() ,求证:
,求证:![]()
(3)如图3,在(2)的条件下,连接![]() 当
当![]() 平分
平分![]() 时,将
时,将![]() 沿着
沿着![]() 折至
折至![]() 探究
探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com