
【题目】如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
【答案】:解:(1)∵△ABC与△DCE是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠ECB+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS);
(2)过点C作CH⊥BQ于H,
∵△ABC是等边三角形,AO是角平分线,
∴∠DAC=30°,
∵△ACD≌△BCE,
∴∠QBC=∠DAC=30°,
∴CH=![]() BC=
BC=![]() ×8=4,
×8=4,
∵PC=CQ=5,CH=4,
∴PH=QH=3,
∴PQ=6.
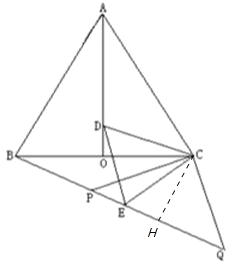
【解析】:(1)由△ABC与△DCE是等边三角形,可得AC=BC,DC=EC,∠ACB=∠DCE=60°,又由∠ACD+∠DCB=∠ECB+∠DCB=60°,即可证得∠ACD=∠BCE,所以根据SAS即可证得△ACD≌△BCE;
(2)首先过点C作CH⊥BQ于H,由等边三角形的性质,即可求得∠DAC=30°,则根据等腰三角形与直角三角形中的勾股定理即可求得PQ的长.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
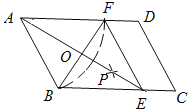
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的 ![]() 的概率是 .
的概率是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,为减少交叉感染,催生了以智能技术为支撑的无接触服务.某快递公司准备购进![]() ,
,![]() 两种型号的智能机器人送快递.经市场调査发现,
两种型号的智能机器人送快递.经市场调査发现,![]() 型号机器人的单价比
型号机器人的单价比![]() 型号机器人贵600元,3台
型号机器人贵600元,3台![]() 型号机器人比2台
型号机器人比2台![]() 型号机器人贵1200元.
型号机器人贵1200元.
(1)求![]() ,
,![]() 两种型号机器人的单价各是多少元?
两种型号机器人的单价各是多少元?
(2)若该快递公司准备用不超过132000元购进![]() ,
,![]() 两种型号机器人共50台,请问该快递公司最多可购进
两种型号机器人共50台,请问该快递公司最多可购进![]() 型号机器人多少台?
型号机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弦BE与弦CD交于点G,点E为 ![]() 的中点,过点B的直线交DC延长线于点A,AB∥DE.
的中点,过点B的直线交DC延长线于点A,AB∥DE.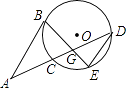
(1)若AB=AG,求证:AB是⊙O切线;
(2)在(1)条件下,若tanA= ![]() ,DE=10,求⊙O的半径.
,DE=10,求⊙O的半径.
(3)求证:AG2﹣BG2=ACAG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线
为直线![]() 上一点,
上一点,![]()

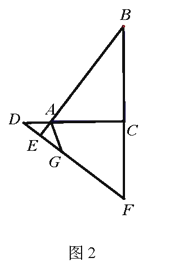

(1)如图1,当![]() 在
在![]() 上,
上,![]() 在
在![]() 上时,求证
上时,求证![]() ;
;
(2)如图2,当![]() 在
在![]() 的延长线上,
的延长线上,![]() 在
在![]() 的延长线上时,点
的延长线上时,点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() ,求证:
,求证:![]()
(3)如图3,在(2)的条件下,连接![]() 当
当![]() 平分
平分![]() 时,将
时,将![]() 沿着
沿着![]() 折至
折至![]() 探究
探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
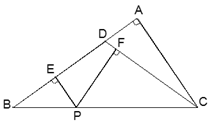
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
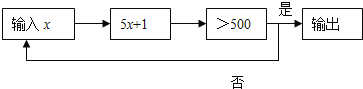
【题目】按下面程序计算,即根据输入的![]() 判断
判断![]() 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的![]() 的值作为新的
的值作为新的![]() 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入![]() 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有![]() 的值是__.
的值是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com