
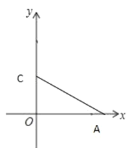
【题目】在直角坐标系中,已知![]() 、
、![]() ,
,![]() ,在
,在![]() 的边上取两点
的边上取两点![]() 、
、![]() (点
(点![]() 是不同于点
是不同于点![]() 的点),若以
的点),若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,则符合条件的点
全等,则符合条件的点![]() 的坐标为__________.
的坐标为__________.
【答案】![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
先求出AC直线解析式,再根据题意分情况作图,根据坐标特点即可求解.
∵![]() ,
,![]()
∴CO=![]() ,AO=6,AC=4
,AO=6,AC=4![]()
∴∠CAO=30°,
设直线AC为y=kx+b
把A,C代入直线得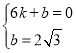
解得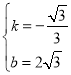
∴直线AC为:y=![]() x+
x+![]()
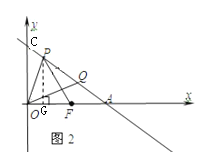
如图1,当OP平分∠CPF时,△OFP≌△OQP,
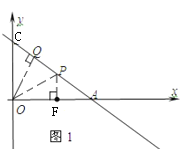
∵![]() ,∴P点横坐标为3,
,∴P点横坐标为3,
故P![]()
如图2,当AO=AP,OF=PQ时,△OFP≌△PQO,
作PG⊥AO,∵AP=AO=6,∠CAO=30°,
∴PG=![]() AP=3,
AP=3,
∴P点纵坐标为3,代入直线AC得P![]() ,
,
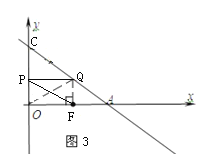
如图3,当P,Q分别是CO,AC中点时,PQ=OF,PO=QF,△OFP≌△PQO,
∴OP=![]() CO=
CO=![]()
∴P![]() ,
,
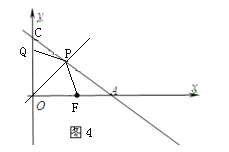
如图4,当P点在第一象限角平分线时,QP=FP,OF=OQ,△OFP≌△OQP
把x=y代入直线AC得,x=y=![]()
∴P![]()
综上:P点坐标为![]() ,
,![]() ,
,![]() ,
,![]()
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B(m,﹣2).
的图象交于点A(1,4)和点B(m,﹣2).

(1)求一次函数的关系式;
(2)求△AOB的面积;
(3)观察图象,写出使得y1≤y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(多选)在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
地到![]() 地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离
地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系,下列说法正确的是( )
(小时)的函数关系,下列说法正确的是( )

A.甲乙两车出发2小时后相遇
B.甲车速度是40千米/小时
C.相遇时乙车距离![]() 地100千米
地100千米
D.乙车到![]() 地比甲车到
地比甲车到![]() 地早
地早![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店计划购进![]() ,
,![]() 两种笔记本共60本,每本
两种笔记本共60本,每本![]() 种笔记本比
种笔记本比![]() 种笔记本的利润高3元,销售2本
种笔记本的利润高3元,销售2本![]() 种笔记本与3本
种笔记本与3本![]() 种笔记本所得利润相同,其中
种笔记本所得利润相同,其中![]() 种笔记本的进货量不超过进货总量的
种笔记本的进货量不超过进货总量的![]() ,
,![]() 种笔记本的进货量不少于30本.
种笔记本的进货量不少于30本.
(1)每本![]() 种笔记本与
种笔记本与![]() 种笔记本的利润各为多少元?
种笔记本的利润各为多少元?
(2)设购进![]() 种笔记本
种笔记本![]() 本,销售总利润为
本,销售总利润为![]() 元,文具店应如何安排进货才能使得
元,文具店应如何安排进货才能使得![]() 最大?
最大?
(3)实际进货时,![]() 种笔记本进价下降
种笔记本进价下降![]() (
(![]() )元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案.
)元.若两种笔记本售价不变,请设计出笔记本销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011内蒙古赤峰,7,3分)早晨,小张去公园晨练,下图是他离家的距离y(千
米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是 ( )

A.小张去时所用的时间多于回家所用的时间B.小张在公园锻炼了20分钟
C.小张去时的速度大于回家的速度 D.小张去时走上坡路,回家时走下坡路
查看答案和解析>>
科目:初中数学 来源: 题型:
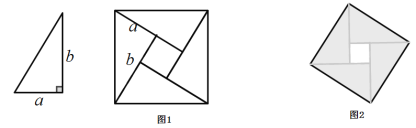
【题目】我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:
(1)叙述勾股定理(用文字及符号语言叙述);
(2)证明勾股定理;
(3)若大正方形的面积是![]() ,小正方形的面积是
,小正方形的面积是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
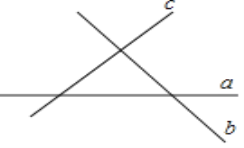
【题目】如图,有3条公路a、b、c两两相交,现在要修建加气站,使得加气站到3条公路的距离都相等.(1)满足条件的加气站共有 处.(2)请你找出加气站P的位置,要求:①找出一个加气站P的位置即可;②尺规作图,保留作图痕迹,不写做法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com