
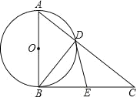
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连结DE、OE.
(1)判断DE与⊙O的位置关系,并说明理由.
(2)求证:BC2=2CDOE.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)连接OD,根据直角三角形中线性质和圆周角定理可得∠ODE=90°;(2)连接OE,根据三角形中位线性质证△ABC∽△BDC,BC2=2CDOE.
(1)证明:连接OD,
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE= BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,即∠C+∠A=90°,
∴∠ADO+∠CDE=90°,即∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为圆O的切线;
(2)证明:连接OE,
∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,∴AC=2OE
∵∠C=∠C,∠ABC=∠BDC=90°,
∴△ABC∽△BDC,.
BC2=2CDOE.;


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.
(千米)的函数图象.
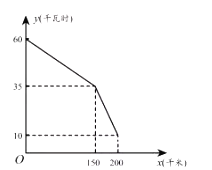
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当![]() 时,求1千瓦时的电量汽车能行驶的路程;
时,求1千瓦时的电量汽车能行驶的路程;
(2)当![]() 时求
时求![]() 关于
关于![]() 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
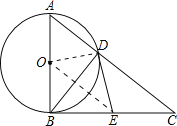
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
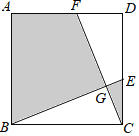
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
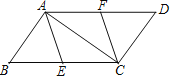
【题目】已知点E、F分别是ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,求AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的侧面示意图.已知铁架水平横管![]() 平行于水平线AD,长为
平行于水平线AD,长为![]() 的真空管
的真空管![]() 与水平线
与水平线![]() 的夹角为37°,铁架
的夹角为37°,铁架![]() 的倾斜角
的倾斜角![]() 为22°,铁架竖直管
为22°,铁架竖直管![]() 的长度为05
的长度为05 ![]() ,根据以上信息,请求出:
,根据以上信息,请求出:

(1))真空管上端![]() 到水平线
到水平线![]() 的距离;
的距离;
(2)水平横管![]() 的长度(结果精确到0.1
的长度(结果精确到0.1 ![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() ,
,![]() 的中线
的中线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.

(1)求圆心![]() 的坐标;
的坐标;
(2)若直线![]() 与
与![]() 相切于点
相切于点![]() ,交
,交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的函数表达式;
的函数表达式;
(3)在过点![]() 且以圆心
且以圆心![]() 为顶点的抛物线上有一动点
为顶点的抛物线上有一动点![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() .若以
.若以![]() 为半径的
为半径的![]() 与直线
与直线![]() 相交于另一点
相交于另一点![]() .当
.当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
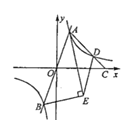
【题目】如图,过原点的直线与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限点
在第一象限点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.![]() 为
为![]() 的平分线,过点
的平分线,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() .若
.若![]() ,
,![]() 的面积为8,则
的面积为8,则![]() 的值为________.
的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com