
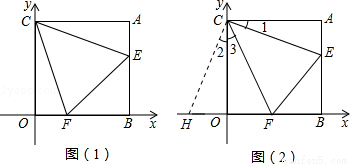
(本题12分)如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,m),A(n,m),且(m–4)2+n2–8n=–16,过C点作∠ECF分别交线段AB、OB于E、F两点.

(1)求A点的坐标.(3分)
(2)若OF+BE=AB,求证:CF=CE.(4分)
(3)如图(2),若∠ECF=45°,给出两个结论:?OF+AE–EF的值不变;?OF+AE+EF的值不变.其中有且只有一个结论正确,请你判断出正确的结论,并加以证明和求出其值(5分).

(1)A(3,3),B(3,0),C(0,3);
(2)证明见解析;
(3)结论①正确,即OF+AE﹣EF的值不变.
【解析】
试题分析:(1)已知等式变形后,利用非负数的性质求出m与n的值,即可确定出A,B,C的坐标;
(2)由AE+EB=AB,以及OF+BE=AB,得到AE=OF,根据四边形ABOC为正方形,得到CA=CO,且∠A=∠COF=90°,利用SAS得到三角形ACE与三角形OCF全等,利用全等三角形对应边相等得到CF=CE;
(3)结论①正确,即OF+AE﹣EF的值不变,理由为:在x轴负半轴上取点H,使OH=AE,连接CH,利用SAS得到三角形ACE与三角形OCH全等,利用全等三角形对应边相等得到EC=HC,∠1=∠2,根据∠ACO=90°,∠ECF=45°,得到∠1+∠3=45°,等量代换得到∠2+∠3=45°,即∠ECF=∠HCF,利用SAS得到三角形ECF与三角形HCF全等,利用全等三角形对应边相等得到EF=HF,而HF=OH+OF,等量代换得到EF=AE+OF,即AE+OF﹣EF=0.
试题解析:(1)将(m﹣3)2+n2=6n﹣9变形得:(m﹣3)2+(n﹣3)2=0,
∴m=3,n=3,
∴A(3,3),B(3,0),C(0,3);
(2)∵OF+BE=AB,AE+EB=AB,
∴AE=OF,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COF=90°,
在△ACE和△OCF中,
 ,
,
∴△ACE≌△OCF(SAS),
∴CF=CE;
(3)结论①正确,即OF+AE﹣EF的值不变,理由为:
在x轴负半轴上取点H,使OH=AE,连接CH,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COH=90°,
在△ACE和△OCH中,
 ,
,
∴△ACE≌△OCH(SAS),
∴∠1=∠2,EC=HC,
∵∠ACO=90°,∠ECF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=45°,即∠ECF=∠HCF,
在△ECF和△HCF中,
 ,
,
∴△ECF≌△HCF(SAS),
∴EF=HF=HO+OF=AE+OF,
则OF+AE﹣EF=0.
考点:四边形综合题


科目:初中数学 来源:2014-2015学年江苏省八年级上学期第二次月考数学试卷(解析版) 题型:解答题
在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在备用图中画出4个这样的△DEF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省济南市九年级上学期期末竞赛数学试卷(解析版) 题型:选择题
身高1.6米的小芳站在一棵树下照了一张照片,小明量得照片上小芳的高度是1.2厘米,树的高度为6厘米,则树的实际高度大约是( )
A.8米 B.4.5米 C.8厘米 D.4.5厘米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省富阳市八年级10月月考数学试卷(解析版) 题型:填空题
我国传统木结构房屋,窗子常用各种图案装饰,如图是一种常见的图案,这个图案有 条对称轴.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省富阳市八年级10月月考数学试卷(解析版) 题型:选择题
如图,一副分别含有30º和45º角的两块直角三角板,拼成如上图形,其中∠C=90º,∠B=45º,∠E=30º,则∠BFD的度数是( )
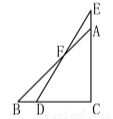
A.15º B.25º C.30º D.10º
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安岳池白庙责任区八年级12月联考数学试卷(解析版) 题型:解答题
(本题8分)如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC ;(2)试判断△OEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安岳池白庙责任区八年级12月联考数学试卷(解析版) 题型:填空题
若多项式x2+ax+b分解因式的结果为(x+1)(x-2),则a+b的值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市七年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题7分)世博会某国国家馆模型的平面图如图所示,其外框是一个大正方形,中间四个大小相同的小正方形(阴影部分)是支撑展馆的核心筒,标记了字母的五个大小相同的正方形是展厅,剩余的四个大小相同的休息厅,已知核心筒的正方形边长比展厅的正方形边长的一半多1米.
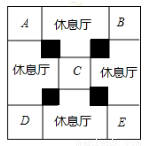
(1)若设展厅的正方形边长为x米,用含x的代数式表示核心筒的正方形边长为 米.
(2)若设核心筒的正方形边长为y米,求该模型的平面图外框大正方形的周长及每个休息厅的图形周长.(用含y的代数式表示)
(3)若设核心筒的正方形边长为2米,求该国家展厅(除四根核心筒)的占地面积。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰兴市七年级上学期期中考试数学试卷(解析版) 题型:填空题
2014年 1至9月份,泰兴市公共财政预算收入累计完成33.81亿元,可用科学记数法表示为____
元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com