Question

6．在平面直角坐标系中，O为原点，点A（-2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．

（1）如图②，当α=90°时，求AE′，BF′的长；
（2）如图③，当0°＜α＜180°时，AE′和BF′有什么位置关系；
（3）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．

Answer 1

分析 （1）先求出OE=OF=1，再判断出△AOE'≌△BOF'，最后用勾股定理求出AE'即可得出结论；
（2）先判断出△AOE'≌△BOF'，得出∠OAE'=∠OBF'，再用∠OAE'+∠ANO=90°，即可得出结论；
（3）先判断出点D'在第一象限内，点D'和P重合时，点P的纵坐标最大，再确定出AE'=$\sqrt{3}$，最后构造直角三角形即可得出结论．

解答 解：（1）∵A（-2，0），B（0，2），
∴OA=OB=2，
∵点E，F是OE，OF的中点，
∴OE=OF=1，
由旋转知，∠EOE'=∠FOF'，
∴OE'=OE，OF'=OF'，
∴OE'=OF'，
∵OA=OB，
∴△AOE'≌△BOF'，
∴AE'=BF'，
当α=90°时，点E'和点F重合，
在Rt△AOE'中，AO=2，E'O=1，根据勾股定理得，AE'=$\sqrt{A{O}^{2}+E'{O}^{2}}$=$\sqrt{5}$，
∴BF'=AE'=$\sqrt{5}$；

（2）AE'⊥BF'，
理由：如图1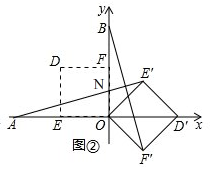，由旋转知，∠EOE'=∠FOF'，
∴OE'=OE，OF'=OF'，
∴OE'=OF'，
∵OA=OB，
∴△AOE'≌△BOF'，
∴∠OAE'=∠OBF'，
∵∠OAE'+∠ANO=90°，∠ANO=∠BNE'，
∴∠OBF'+∠BNE'=90°，
∴AE'⊥BF'；

（3）如图2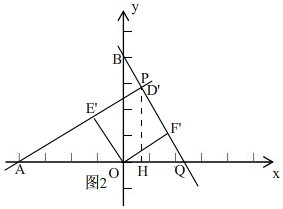，在第一象限内，当点D'与点P重合时，点P的纵坐标最大，
过点P作OH⊥x轴于H，
∵∠AE'O=90°，E'O=1，AO=2，
∴∠E'AO=30°，AE'=$\sqrt{3}$，
∴AP=AE'+D'E'=$\sqrt{3}$+1，
在Rt△APH中，∠PAH=30°，
∴PH=$\frac{1}{2}$AP=$\frac{\sqrt{3}+1}{2}$，
∴点P的纵坐标的最大值为$\frac{\sqrt{3}+1}{2}$．

点评 此题是一次函数综合题，主要考查了全等三角形的判定和性质，旋转的性质，勾股定理，解（1）的关键是构造直角三角形AME，解（2）的关键是得出∠OAE'=∠OBF'，解（3）的关键是判断出点D'和P重合时，点P的纵坐标最大，是一道常规题．