
 ��ͼ��ֱ������ϵxOy�У�A��0��5����ֱ��x=-5��x�ύ�ڵ�D��ֱ��y=-$\frac{3}{8}$x-$\frac{39}{8}$��x�ἰֱ��x=-5�ֱ��ڵ�C��E����B��E����x��Գƣ�����AB��
��ͼ��ֱ������ϵxOy�У�A��0��5����ֱ��x=-5��x�ύ�ڵ�D��ֱ��y=-$\frac{3}{8}$x-$\frac{39}{8}$��x�ἰֱ��x=-5�ֱ��ڵ�C��E����B��E����x��Գƣ�����AB������ ��1�������������ϵ���ص�ȷ������C�����꣬������ֱ�ߵĽ��������ȷ�����������E���꣬�����õ���B���꣬����ô���ϵ�������ֱ��AB����ʽ��
��2��ֱ������ֱ�������ε�������㷽����ֱ�����ε�����ļ��㼴�ɵó����ۣ�
��3�������ֱ��AB��x��Ľ������꣬�жϳ���C����ֱ��AB�ϣ����ɣ�
��� �⣺��1����ֱ��y=-$\frac{3}{8}$x-$\frac{39}{8}$�У�
��y=0������0=-$\frac{3}{8}$x-$\frac{39}{8}$��
��x=-13��
��C��-13��0����
��x=-5������y=-$\frac{3}{8}$����-5��-$\frac{39}{8}$=-3��
��E��-5��-3����
�ߵ�B��E����x��Գƣ�
��B��-5��3����
��A��0��5����
����ֱ��AB�Ľ���ʽΪy=kx+5��
��-5k+5=3��
��k=$\frac{2}{5}$��
��ֱ��AB�Ľ���ʽΪy=$\frac{2}{5}$x+5��
��2���ɣ�1��֪��E��-5��-3����
��DE=3��
��C��-13��0����
��CD=-5-��-13��=8��
��S��CDE=$\frac{1}{2}$CD��DE=12��
������֪��OA=5��OD=5��BD=3��
��S�ı���ABDO=$\frac{1}{2}$��BD+OA����OD=20��
��S=S��CDE+S�ı���ABDO=12+20=32��
��3���ɣ�2��֪��S=32��
�ڡ�AOC�У�OA=5��OC=13��
��S��AOC=$\frac{1}{2}$OA��OC=$\frac{65}{2}$=32.5��
��S��S��AOC��
���ɣ��ɣ�1��֪��ֱ��AB�Ľ���ʽΪy=$\frac{2}{5}$x+5��
��y=0����0=$\frac{2}{5}$x+5��
��x=-$\frac{25}{2}$��-13��
���C����ֱ��AB�ϣ�
������A��B��C����ͬһ��ֱ���ϣ�
��S��AOC��S��
���� ������һ�κ����ۺ��⣬��Ҫ�������������ϵ���ص㣬�ԳƵ����ʣ�����ϵ�����������Σ�ֱ�����ε�����ļ��㣬�⣨1���Ĺؼ���ȷ������C��E�����꣬�⣨2���Ĺؼ������⼸��ͼ�ε�����ļ��㣬�⣨3���Ĺؼ���ȷ����ֱ��AB��x��Ľ������꣬��һ�������⣮


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
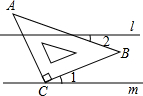 ��ͼ��ֱ��l��m��������45��ǵ����ǰ�ABC��ֱ�Ƕ���C����ֱ��m�ϣ�����1=20�㣬���2�Ķ���Ϊ25�ȣ�
��ͼ��ֱ��l��m��������45��ǵ����ǰ�ABC��ֱ�Ƕ���C����ֱ��m�ϣ�����1=20�㣬���2�Ķ���Ϊ25�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪AMΪ��O��ֱ����ֱ��BC������M����AB=AC����BAM=��CAM���߶�AB��AC�ֱ�O�ڵ�D��E����BMD=40�㣬���EOM=80�㣮
��ͼ����֪AMΪ��O��ֱ����ֱ��BC������M����AB=AC����BAM=��CAM���߶�AB��AC�ֱ�O�ڵ�D��E����BMD=40�㣬���EOM=80�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ���� | B�� | ���� | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
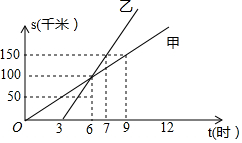 ��ͼ�Ǽס������˴�ͬһ�ص������·��s��ǧ�ף���ʱ��t��ʱ���仯��ͼ��
��ͼ�Ǽס������˴�ͬһ�ص������·��s��ǧ�ף���ʱ��t��ʱ���仯��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com