
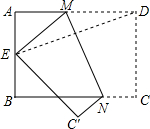
 如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.
如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$. 分析 如图,作辅助线;首先运用勾股定理、翻折变换的性质等几何知识求出AM、BN、CN的长度,然后借助三角形的面积公式列出关于线段MN的方程,求出MN即可解决问题.
解答 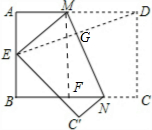 解:如图,过M作MF⊥BC,垂足为F;
解:如图,过M作MF⊥BC,垂足为F;
∵四边形ABCD为矩形,且点E为AB的中点,
∴∠B=∠C=∠A=90°,DC=AB=6,
AD=BC=8,AE=3,
由勾股定理得:DE=$\sqrt{73}$;
再由翻折的性质可知MN垂直平分DE,
故∠MGD=90°,∠NMD+∠GDM=90°
又易知MF⊥AD,即∠FMN+∠NMD=90°
∴∠GDM=∠FMN,
∴Rt△EAD∽Rt△NFM
则有$\frac{MN}{DE}=\frac{MF}{DA}$
求得MN=$\frac{3\sqrt{73}}{4}$.
故答案为$\frac{3\sqrt{73}}{4}$.
点评 该题主要考查了翻折变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用翻折变换的性质等几何知识点来分析、判断、解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
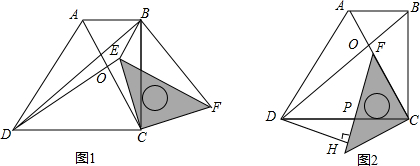
 如图,在△ABC中,∠ACB=90°,△CAD≌△CED,△CEF≌△BEF,△CEF≌△CAD.
如图,在△ABC中,∠ACB=90°,△CAD≌△CED,△CEF≌△BEF,△CEF≌△CAD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
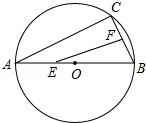 如图,AB是⊙O的直径,弦AC=8cm,BC=6cm,若动点E以2cm/s的速度从A向B运动,点F以1cm/s的速度从B向C运动,设运动时间为t(s),连接EF,当△BEF是直角三角形时,求t(s)的值.
如图,AB是⊙O的直径,弦AC=8cm,BC=6cm,若动点E以2cm/s的速度从A向B运动,点F以1cm/s的速度从B向C运动,设运动时间为t(s),连接EF,当△BEF是直角三角形时,求t(s)的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-2b | B. | a | C. | -a+2b | D. | -a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-4}$$\sqrt{-16}$=(-2)(-4)=8 | B. | $\sqrt{8{a^2}}=4a(a>0)$ | C. | $\sqrt{{3^2}+{4^2}}=3+4=7$ | D. | ($\sqrt{3}$+2)2=7+4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com