
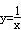 的图象与抛物线y=x2+(k2﹣3k﹣4)x+2k从左至右交于Q、R、S三点,且Q的坐标(﹣1,﹣1),R的坐标(
的图象与抛物线y=x2+(k2﹣3k﹣4)x+2k从左至右交于Q、R、S三点,且Q的坐标(﹣1,﹣1),R的坐标(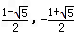 ),S的坐标(
),S的坐标(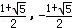 ),求四边形AQBS的面积;
),求四边形AQBS的面积;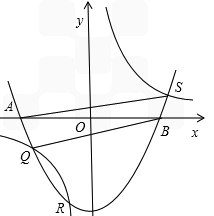
解:(1)设A点坐标为(x1,0),B点坐标为(x2,0),
∵A、B两点关于原点对称,
∴x1+x2=0,又x1+x2=﹣(k2﹣3k﹣4),
则k2﹣3k﹣4=0,
解得k1=﹣1,k2=4,
当k=4时,抛物线为y=x2+8,
此时△=﹣32<0,舍去;
当k=﹣1时,抛物线为y=x2﹣2,
此时△=8>0,则抛物线与x轴交于两点,
故所求k值为﹣1;
(2)由(1)知A(-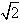 ,0),B(
,0),B(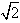 ,0),
,0),
∴AB=2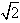 ,
,
则四边形AQBS的面积为:
S△AQB+S△ASB=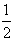 ·AB|﹣1|+
·AB|﹣1|+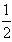 AB|
AB|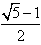 |=
|=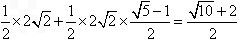 ;
;
(3)∵抛物线的顶点坐标为(0,﹣2),
假设满足条件的点P存在,
则∵S△PAB=2S△RAB,
∴点P的纵坐标为:2×(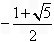 )=﹣1﹣
)=﹣1﹣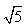 ,
,
而﹣1﹣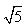 <﹣2,
<﹣2,
∴P点不存在.即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)求b+c的值;
(1)求b+c的值;查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com