解:(1)∵点A(-1,0)、B(3,0)在抛物线y=ax
2+bx+3上,
∴
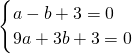
,
解得a=-1,b=2,
∴抛物线的解析式为:y=-x
2+2x+3.
(2)在抛物线解析式y=-x
2+2x+3中,令x=0,得y=3,∴C(0,3).
设直线BC的解析式为y=kx+b,将B(3,0),C(0,3)坐标代入得:

,
解得k=-1,b=3,
∴y=-x+3.
设E点坐标为(x,-x
2+2x+3),则P(x,0),F(x,-x+3),
∴EF=y
E-y
F=-x
2+2x+3-(-x+3)=-x
2+3x.
∵四边形ODEF是平行四边形,
∴EF=OD=2,
∴-x
2+3x=2,即x
2-3x+2=0,
解得x=1或x=2,
∴P点坐标为(1,0)或(2,0).
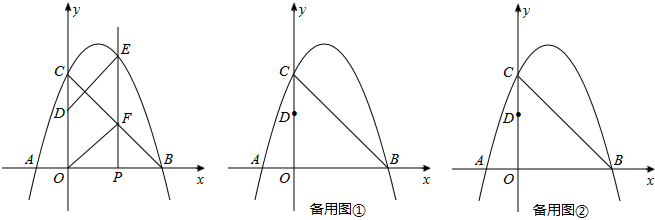
(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点A与?ODEF对称中心的直线平分?ODEF的面积.
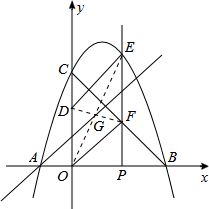
①当P(1,0)时,
点F坐标为(1,2),又D(0,2),
设对角线DF的中点为G,则G(

,2).
设直线AG的解析式为y=kx+b,将A(-1,0),G(

,2)坐标代入得:
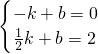
,
解得k=b=

,
∴所求直线的解析式为:y=

x+

;
②当P(2,0)时,
点F坐标为(2,1),又D(0,2),
设对角线DF的中点为G,则G(1,

).
设直线AG的解析式为y=kx+b,将A(-1,0),G(1,

)坐标代入得:
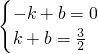
,
解得k=b=

,
∴所求直线的解析式为:y=

x+

.
综上所述,所求直线的解析式为:y=

x+

或y=

x+

.
分析:(1)利用待定系数法求出抛物线的解析式;
(2)平行四边形的对边相等,因此EF=OD=2,据此列方程求出点P的坐标;
(3)本问利用中心对称的性质求解.平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点A与?ODEF对称中心的直线平分?ODEF的面积.
点评:本题是二次函数的综合题型,考查了二次函数的图象与性质、待定系数法、平行四边形的性质、中心对称的性质等知识点.第(3)问中,特别注意要充分利用平行四边形中心对称的性质,只要求出其对称中心的坐标,即可利用待定系数法求出所求直线的解析式.

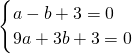 ,
, ,
,
 ,2).
,2). ,2)坐标代入得:
,2)坐标代入得: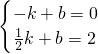 ,
, ,
, x+
x+ ;
; ).
). )坐标代入得:
)坐标代入得: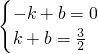 ,
, ,
, x+
x+ .
. x+
x+ 或y=
或y= x+
x+ .
.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).