练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，下列条件中，能判断直线L1∥L2的是( )

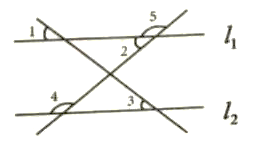
    A. ∠2=∠3 B. ∠l=∠3 C. ∠4+∠5=180 D. ∠2=∠4

    【答案】B

    【解析】平行线的判定定理有：①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行．根据以上内容判断即可．

    A.∠2和∠3不是直线L1、L2被第三条直线所截形成的角,故不能判断直线L1∥L2；

    B.∵∠1=∠3,∴L1∥L2 (同位角相等两直线平行)；

    C.∠4、∠5是直线L1、L2被第三条直线所截形成的同位角,故∠4+∠5=180不能判断直线L1∥L2.

    D.∠2、∠4是直线L1、L2被第三条直线所截形成的同旁内角,故∠2=∠4不能判断直线L1∥L2.

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

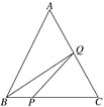
    【题目】在△ABC中，已知AB＝BC＝CA＝4 cm，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1 cm/s；点Q沿CA、AB向终点B运动，速度为2 cm/s，设它们运动的时间为x(s)，当x＝__________，△BPQ是直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是以BC为直径的半圆O的切线，D为半圆上一点，AD=AB，AD、BC的延长线相交于点E．
    （1）求证：AD是半圆O的切线；
    （2）连结CD，求证：∠A=2∠CDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算题3tan30°﹣|﹣2|+ +（﹣1）2017；
    （1）计算：3tan30°﹣|﹣2|+ +（﹣1）2017；
    （2）解方程： = ﹣2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=﹣ x+6的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．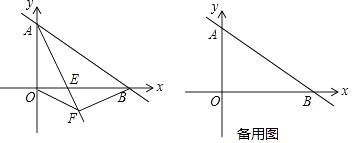

    （1）求点B的坐标；
    （2）求直线AE的表达式；
    （3）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图①，已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

    （2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知x>0，现规定符号[x]表示大于或等于x的最小整数，如[0.5]＝1，[4.3]＝5，[6]＝6……

    (1)填空：[]＝_____，[8.05]＝______；若[x]＝5，则x的取值范围是________．

    (2)某市的出租车收费标准如下：3 km以内(包括3km)收费5元，超过3 km的，每超过1km，加收1.2元(不足1 km按1 km计算)．设所行驶的路程为x(km)，用含[x]的式子表示出当x>3时的乘车费用．

    (3) 在(2)的条件下，某乘客乘出租车后付费18.2元，求该乘客所乘路程的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案：

    　　　　 　

    ⑴ 当黑砖n＝1时，白砖有_______块，当黑砖n＝2时，白砖有________块，

    当黑砖n＝3时，白砖有_______块．

    ⑵ 第n个图案中，白色地砖共 块．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠CAB=∠DBA，添加下列某条件，未必能判定△ABC≌BAD的是（ ）

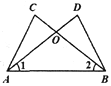
    A. AC=BD B. AD=BC C. ∠l=∠2 D. ∠C=∠D

    查看答案和解析>>

    同步练习册答案