
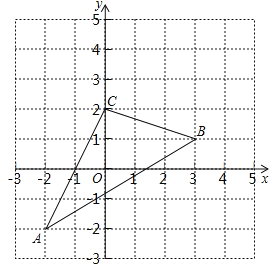
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向左平移1个单位得到△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△ABC的面积.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.易证∠EHF=∠EGF=∠GEH=90°,从而可知四边形EGFH是矩形.
小明继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
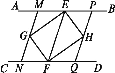
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形.要证平行四边形MNQP是菱形,只要证MN=NQ.由已知条件_____,MN∥EF,可得NG=NF,故只要证GM=FQ,即证△MGE≌△QFH.易证_____,_____,故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,_____,即可得证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
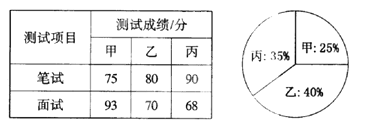
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如扇形图所示,每得一票记作1分.
(l)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )?
(2)根据实际需要,单位将笔试、面试、民主评议三项测试得分按5 : 2 : 3的比例确定个人成绩,那么谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.
(1)求大本作业本与小本作业本每本各多少元?
(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
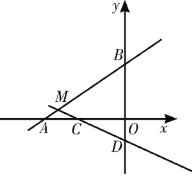
【题目】如图,在平面直角坐标系xOy中,已知直线AB:y=![]() x+4交x轴于点A,交y轴于点B.直线CD:y=-
x+4交x轴于点A,交y轴于点B.直线CD:y=-![]() x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标.
(2)若点P是射线MD的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系,并指出x的取值范围.
(3)当S=10时,平面直角坐标系内是否存在点E,使以点B,E,P,M为顶点的四边形是平行四边形?若存在,共有几个这样的点?请求出其中一个点的坐标(写出求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
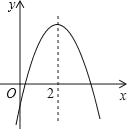
A. ac<0 B. ab>0 C. 4a+b=0 D. a﹣b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
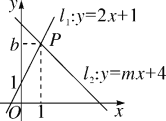
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com