
����Ŀ����֪��ABC�ǵ��������Σ���BAC=90����CD=![]() BC��DE��CE��DE=CE������AE����M��AE���е�.
BC��DE��CE��DE=CE������AE����M��AE���е�.
��1����ͼ1������D��BC���ϣ�����CM����AB=4ʱ����CM�ij���
��2����ͼ2������D����ABC���ڲ�������BD����N��BD�е㣬����MN��NE����֤MN��AE��
��3����ͼ3����ͼ2�е���CDE�Ƶ�C��ʱ����ת��ʹ��BCD=30��������BD����N��BD�е㣬����MN��̽��![]() ��ֵ��ֱ��д�����
��ֵ��ֱ��д�����

���𰸡���1��![]() ����2��֤�����̼���������3��
����2��֤�����̼���������3��![]() .
.
��������
�����������1�����ݵ���ֱ��������ABC�ó�BC�ij��ȣ�Ȼ����ݵ���ֱ��������DCE�ó�CE�ij��ȣ�Ȼ�����Rt��ACE�Ĺ��ɶ����ó�AE�ij��ȣ��Ӷ�����ֱ��������б���ϵ����ߵ���б�ߵ�һ��ó��𰸣���2���ӳ�EN��NF��ʹNE=NF��������BF��AF��Ȼ��֤����ABF�ա�ACE���Ӷ��ó���FAE=��BAC=90����Ȼ�����ƽ���ߵ����ʵó��𰸣���3�����ݵڶ���ͬ���ķ����ó�MN=![]() AF��AF=AE���Ӷ��ó���.
AF��AF=AE���Ӷ��ó���.
�����������1����AB=AC=4 ��BAC=90�� ��BC=4![]() ��CD=2
��CD=2![]() ��CE=2��
��CE=2��
����Rt��ACE�Ĺ��ɶ����ɵã�AE=![]() ��CM=
��CM=![]()
��2����ͼ���ӳ�EN��NF��ʹNE=NF��������BF��AF��
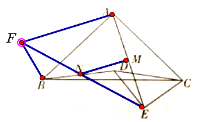
�ɵ�BF=DE=CE����FBN=��NDE�� ����ACE=90��-��DCB
��ABF=��BDE-��ABN=��180��-��DBC-��DCB-��EDC-��ABN=180��-����DBC+��ABN��-45��-��DCB=90��-��DCB
������ACE=��ABF��������ABF�ա�ACE�� ������FAB=��EAC�� ������FAE=��BAC=90����
��ΪMN//AF������MN��AE��
��3��ͬ��2���ɵ�MN=![]() AF��AF=AE��
AF��AF=AE��
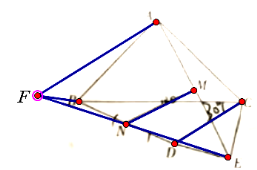
��AC=2CE����ACE=120���������AE=![]() �� ����
�� ����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y��4x��2�ĺ���ֵy���Ա���xֵ�������_____�������С������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ľ��붼��ȵĵ�����������εģ�������
A. �����ߵĽ��� B. ������ƽ���ߵĽ���
C. �������ߵĽ��� D. �����ߵĴ�ֱƽ���ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����һ�������ص㣺0��1��-4��9��-16��25���������11�������� ��
A��-121 B��-100 C.100 D��121
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ�������У��еĺ�������Գ�ͼ��,����4�������У����Կ�������Գ�ͼ�ε����� ��
�� �� �� ��
��A���� ��B���� ��C���� ��D����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ�������������ߵĽ������������ⲿ����ô�����������( )
A. ��������� B. �۽�������
C. ֱ�������� D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ���ı����������ǵ���Ƿֱ���80�㣬85�㣬90�㣬��ô���ĵ��ĸ�����( )
A.105��B.95��C.85��D.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�ǡ�O���ڽ��ı��Σ��ҡ�A�á�B�á�C��1��4��8�����D�Ķ�����( )
A. 10�� B. 30�� C. 80�� D. 100��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��a��b��c�ǡ�ABC���߳�����M=(a��b��c)(a��b��c)(a��b��c)����ô (����)
A. M��0 B. M=0 C. M��0 D. ����ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com