
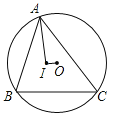
【题目】如图,不等边△ABC内接于![]() ,I是其内心,AI⊥OI,AB=2,BC=3,则AC的长为( )
,I是其内心,AI⊥OI,AB=2,BC=3,则AC的长为( )
A. 4B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
延长AI交⊙O于D,连接OA、OD、BD和BI,可得BD=ID=AI.易证![]() ,则OD⊥BC,作IG⊥AB于G,又∠DBE=∠IAG,则BD=AI,所以Rt△BDE≌Rt△AIG,从而得出AB+AC=2BC,代入数据即可得到结论.
,则OD⊥BC,作IG⊥AB于G,又∠DBE=∠IAG,则BD=AI,所以Rt△BDE≌Rt△AIG,从而得出AB+AC=2BC,代入数据即可得到结论.
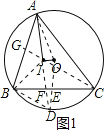
证明:如图1,延长AI交⊙O于D,连接OA、OD、BD和BI,
∵OA=OD,OI⊥AD,
∴AI=ID,
又∠DBI=∠DBC+∠CBI=∠DAC+∠CBI,
=![]() ,
,
因此,BD=ID=AI,
∵I是其内心,
∴AD是∠BAC的平分线,
∴![]()
,∴OD⊥BC,记垂足为E,
∴![]() ,
,
作IG⊥AB于G,∵∠DBE=∠IAG,BD=AI,
∴△BDE≌△AIG(AAS),
∴![]() ,
,
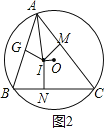
如图2,过O作OM⊥AC,ON⊥BC,
∵I是其内心,
∴AG=AM,CM=CN,BG=BN,
∴AG=AC-CM=AC-(BC-BN)=AC-BC+BN=AC-BC+(AB-AG),
∴![]() ,
,
∴AB+AC=2BC,
∵AB=2,BC=3,
∴AC=4,
故选:A.


科目:初中数学 来源: 题型:
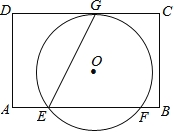
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=
AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(k﹣1)x2+2kx+2=0.
(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是方程(k﹣1)x2+2kx+2=0的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣1)x2+(2k﹣3)x+k+1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为![]() 的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
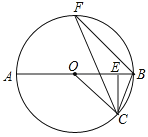
(1)求证:∠OCF=∠ECB;
(2)当AB=10,BC=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅童威准备在一块长为60,宽为48的长方形花圃内修建四条宽度相等,且与各边垂直的小路.四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的8倍.若四条小路所占面积为160.设小路的宽度为x,依题意列方程,化为一般形式为_________
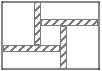
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10 元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于 16 元/件, 市场调查发现,该产品每天的销售量 y (件)与销售价 x (元/件)之间的函数关系如图所示.。
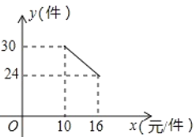
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当每件销售价为多少元时,每天的销售利润为144元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com