
【题目】已知:如图,AB为![]() 的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
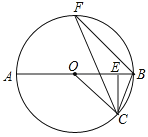
(1)求证:∠OCF=∠ECB;
(2)当AB=10,BC=![]() ,求CF的值.
,求CF的值.
【答案】(1)证明见详解.
(2)![]()
【解析】
(1)延长CE交⊙O于点G,利用圆周角的性质进行解答即可.
(2)连接AC,FO,利用△AOC和△FOC均是等腰三角形并且全等,得到CF=AC,在根据AB为直径,△ABC为直角三角形,利用勾股定理求出AC即可得到CF的长.
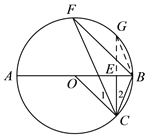
证明:(1)延长CE交⊙O于点G.
∵AB为⊙O的直径,CE⊥AB于E,
∴BC=BG,
∴∠G=∠2,
∵BF∥OC,
∴∠1=∠F,
又∵∠G=∠F,
∴∠1=∠2.
即∠OCF=∠ECB.
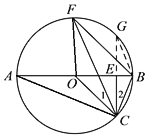
(2)连接AC,FO
∴OA=OC=OF,∠A=∠CFB,
由(1)可知∠1=∠CFB,并△AOC和△FOC均是等腰三角形
∴∠1=∠OFC=∠A=∠ACO
在△AOC和△FOC中
OC是公共边,∠1= =∠ACO,∠OFC=∠A
∴△AOC![]() △FOC
△FOC
∴CF=AC
∵AB为直径
∴![]()
∴![]()
![]()


科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标着数字 ![]() ,
,![]() ,
,![]() ,
,![]() 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.
的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.
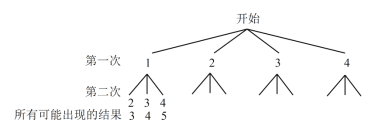
(1)由上图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后 (填"放回"或"不放回"),再随机抽出一张卡片;
(2)帮甲同学完成树状图;
(3)求甲同学两次抽到的数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2经过点A(2,1).
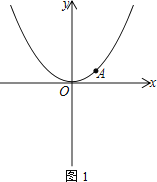
(1) 求a的值;
(2) 如图1,点M为x轴负半轴上一点,线段AM交抛物线于N.若△OMN为等腰三角形,求点N的坐标;
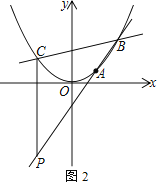
(3) 如图2,直线y=kx-2k+3交抛物线于B、C两点,过点C作CP⊥x轴,交直线AB于点P,请说明点P一定在某条确定的直线上运动,求出这条直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-4(k-1)x+4k2=0有两个实数根x1、x2
(1) 求k的取值范围
(2) 若x1x2-2|x1+x2|=4,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】镇江某特产专卖店销售某种特产,其进价为每千克40元,若按每千克60元出售,平均每天可售出100千克,经过市场调查发现,单价每降低3元,平均每天的销售量可增加30千克,专卖店销售这种特产若想要平均每天获利2240元,且销售尽可能大,则每千克特产应定价为多少元?
(1)解:方法1:设每千克特产应降价x元,由题意,得方程为:_____;
方法2:设每千克特产降低后定价为x元,由题意,得方程为:_____.
(2)请你选择一种方法,写出完整的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com