
【题目】已知关于x的方程x2-4(k-1)x+4k2=0有两个实数根x1、x2
(1) 求k的取值范围
(2) 若x1x2-2|x1+x2|=4,求k的值
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的![]() 型车去年6月份销售总额为3.2万元,今年经过改造升级后
型车去年6月份销售总额为3.2万元,今年经过改造升级后![]() 型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的
型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
![]() ,
,![]() 两种型号车的进货和销售价格表:
两种型号车的进货和销售价格表:
|
| |
进货价格(元 | 1100 | 1400 |
销售价格(元 | 今年的销售价格 | 2400 |
(1)求今年6月份![]() 型车每辆销售价多少元;
型车每辆销售价多少元;
(2)该车行计划7月份新进一批![]() 型车和
型车和![]() 型车共50辆,且
型车共50辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能使这批车获利最多?
型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为![]() 的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
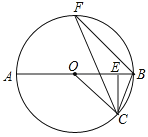
(1)求证:∠OCF=∠ECB;
(2)当AB=10,BC=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=![]() .求证:CB是⊙O的切线.
.求证:CB是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅童威准备在一块长为60,宽为48的长方形花圃内修建四条宽度相等,且与各边垂直的小路.四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的8倍.若四条小路所占面积为160.设小路的宽度为x,依题意列方程,化为一般形式为_________
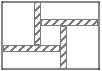
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,P是第一象限角平分线上的一点,且P点的横坐标为3.把一块三角板的直角顶点固定在点P处,将此三角板绕点P旋转,在旋转的过程中设一直角边与x轴交于点E,另一直角边与y轴交于点F,若△POE为等腰三角形,则点F的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(1)求C点坐标,并判断b的正负性;
(2)设这个二次函数的图像的对称轴与直线AC交于点D,已知DC:CA=1:2,直线BD与y轴交于点E,连接BC,
①若△BCE的面积为8,求二次函数的解析式;
②若△BCD为锐角三角形,请直接写出OA的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
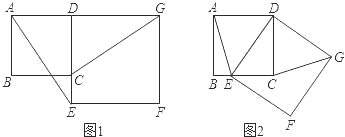
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州旅游文化节开幕前,某凤凰茶叶公司预测今年凤凰茶叶能够畅销,就用32000元购进了一批凤凰茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批凤凰茶叶,所购数量是第一批购进数量的2倍,但每千克凤凰茶叶进价多了10元.
(1)该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com