练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】圆外切等腰梯形的一腰长是8，则这个等腰梯形的上底与下底长的和为（　　）
    A.4
    B.8
    C.12
    D.16

    【答案】D
    【解析】 ∵圆外切等腰梯形的一腰长是8，

    ∴梯形对边和为：8+8=16，

    则这个等腰梯形的上底与下底长的和为16．

    故选：D．

    【考点精析】掌握切线长定理是解答本题的根本，需要知道从圆外一点引圆的两条切线，它们的切线长相等圆心和这一点的连线平分两条切线的夹角．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如下：

    （1）计算“3点朝上”的频率和“5点朝上”的频率；

    （2）小颖说：“根据上述实验，一次实验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”，小颖和小红的说法正确吗？为什么？

    朝上的点数

    1

    2

    3

    4

    5

    6

    出现的次数

    7

    9

    6

    8

    20

    10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC顶点坐标分别是A（0，6），B（﹣3，﹣3），C（1，0），将△ABC平移后顶点A的对应点A1的坐标是（4，10），则点B的对应点B1的坐标为（ ）

    A．（7，1） B．B（1，7） C．（1，1） D．（2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a是最小的正整数，b的相反数还是它本身，c比最大的负整数大3，则（2a+3c）b=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】动手实验：利用矩形纸片(如图1)剪出一个正六边形纸片；再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形) ，如图2．

    (1) 做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少？

    (2) 在(1)的条件下，当矩形的长为2a时，要使无盖正六棱柱侧面积最大，正六棱柱的高为多少？并求此时矩形纸片的利用率为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点

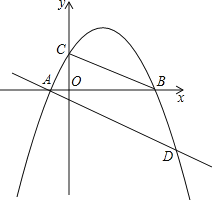
    （1）求这条抛物线的解析式；

    （2）E为抛物线上一动点，是否存在点E使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用配方法解方程x2+8x+7=0，则配方正确的是（ ）
    A.（x﹣4）2=9
    B.（x+4）2=9
    C.（x﹣8）2=16
    D.（x+8）2=57

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求不等式（2x﹣1）（x+3）＞0的解集．

    解：根据“同号两数相乘，积为正”可得：①或 ②．

    解①得x＞；解②得x＜﹣3．

    ∴不等式的解集为x＞或x＜﹣3．

    请你仿照上述方法解决下列问题：

    （1）求不等式（2x﹣3）（x+1）＜0的解集． （2）求不等式≥0的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E、A、C在一条直线上，给出下列三个事项:①AD⊥BC, EG⊥BC，垂足分别为D、G；②∠1=∠2；③AD平分∠BAC．

    （1）以其中两个事项作为条件，另一个事项作为结论，你能组成 个正确的结论；

    （2）请你选择其中一个正确结论进行说明理由．

    解：以 为条件， 为结论．（填写序号）

    理由是：

    查看答案和解析>>

    同步练习册答案