
已知平面直角坐标系中两定点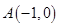 、
、 ,抛物线
,抛物线 过点A,B,与y交于C点,点P(m,n)为抛物线上一点.
过点A,B,与y交于C点,点P(m,n)为抛物线上一点.
(1)求抛物线的解析式和点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)当∠PAB=∠ABC时,求点P的坐标.
解:(1)∵抛物线 过点A,B,
过点A,B,
∴ ,解得:
,解得: ,
,
∴抛物线的解析式为: .
.
∴C .
.
(2)以AB为直径作圆M,与y轴交于点P.则抛物线在圆内的部分,能使∠APB为钝角,
∴M( ,0),⊙M的半径=
,0),⊙M的半径= .
.
∵P是抛物线与y轴的交点,
∴OP=2,
∴MP= 
∴P在⊙M上,
∴由抛物线的对称性可知, ,
,
∴当-1<m<0或3<m<4时,∠APB为钝角.
(3)在Rt△OBC中, .
.
第一种情况:过A作AP∥BC,交抛物线于点P .
∴∠PAB=∠ABC.
过P作PQ⊥AB于Q,
∴ .
.
∵P(m,n),
∴PQ=n,AQ=m+1
∴ .
.
∴ .
.
解得
∴
第二种情况:点P关于x轴的对称点的坐标为
∴直线AP″的解析式为
∴ 解得
解得
∴
∴
解析试题分析:(1)将A点,B点坐标代入解析式,即可求出解析式,可得 C点坐标;(2)以AB为直径作圆M,与y轴交于点P.因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,根据题意可证得P在⊙M上,由抛物线的对称性可知, ,可得-1<m<0,或3<m<4;(3)根据题意分两种情况进行讨论,即可得出答案.
,可得-1<m<0,或3<m<4;(3)根据题意分两种情况进行讨论,即可得出答案.
考点:二次函数综合题.
点评:本题是二次函数的综合题,解答本题的关键是熟练掌握待定系数法求二次函数解析式,学生还要熟练掌握数形结合思想、分类讨论思想的综合应用.本题综合性强,有一定的难度.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
如图,反映的过程是:晓明从家跑步到体育馆,在那里锻炼了一阵后又走到新华书店去买书,然后散步走回家.其中 表示时间(分钟),
表示时间(分钟), 表示晓明离家的距离(千米),那么晓明在体育馆锻炼和在新华书店买书共用去时间是_______________分钟.
表示晓明离家的距离(千米),那么晓明在体育馆锻炼和在新华书店买书共用去时间是_______________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(本题7分)如图, 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
(1)B出发时与A相距 千米。
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时。
(3)B出发后 小时与A相遇。
(4)若B的自行车不发生故障,保持出发时的速度前进, 小时与A相遇?相遇点离B的出发点 千米?在图中表示出这个相遇点C。
(5)A行走的路程S与时间t的函数关系式为 。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
下表给出了代数式 与
与 的一些对应值:
的一些对应值:
 | …… | -2 | -1 | 0 | 1 | 2 | 3 | …… |
 | …… | 5 |  | c | 2 | -3 | -10 | …… |
 ,
, ,
, 的值;
的值; ,直接写出
,直接写出 时
时 的最大值.
的最大值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,抛物线 与
与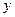 轴交于点
轴交于点 ,与
,与 轴交于
轴交于 、
、 两点,点
两点,点 的坐标为
的坐标为 .
.
(1)求抛物线的解析式及顶点 的坐标;
的坐标;
(2)设点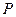 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形 面积相等的四边形
面积相等的四边形 的点
的点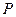 的坐标;
的坐标;
(3)求 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
为支援贫困地区学生,学校开展捐书活动,以下是某学习小组5名学生捐书的册数:3,9,3,7,8,则这组数据的中位数是 ( )
| A.3 | B.7 | C.8 | D.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com