
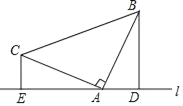
【题目】已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线l的垂线段BD、CE,垂足分别D、E.
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请画出图形,直接给出你的结论(不用证明).
【答案】(1)见解析;(2)上述结论不成立.
【解析】试题分析:(1)由垂线的定义和角的互余关系得出![]()
![]() 由AAS证明
由AAS证明![]() ≌
≌![]() ,得出对应边相等
,得出对应边相等![]() 由
由![]() 即可得出结论;
即可得出结论;
(2)由垂线的定义和角的互余关系得出![]() 由AAS证明
由AAS证明![]() ≌
≌![]() ,得出对应边相等
,得出对应边相等![]() 由
由![]() 之间的和差关系,即可得出结论.
之间的和差关系,即可得出结论.
试题解析:(1)∵∠BAC=![]() ,
,
∴∠BAD+∠CAE=![]() ,
,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=![]() ,
,
∴∠BAD+∠ABD=![]() ,
,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
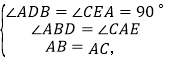
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+AE=DE,
∴BD+CE=DE;
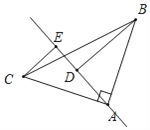
(2)上述结论不成立,
如图所示,BD=DE+CE.
证明:∵∠BAC=![]() ,
,
∴∠BAD+∠CAE=![]() ,
,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=![]() ,
,
∴∠BAD+∠ABD=![]() ,
,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
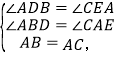
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+DE=AE,
∴BD=DE+CE.
如图所示,CE=DE+BD,
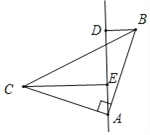
证明:证明:∵∠BAC=![]() ,
,
∴∠BAD+∠CAE=![]() ,
,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=![]() ,
,
∴∠BAD+∠ABD=![]() ,
,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
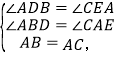
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE+DE=AD,
∴CE=DE+BD.


科目:初中数学 来源: 题型:
【题目】为了解中学生“平均每天体育锻炼时间”的情况,某地区教育部门随机调查了若干名中学生,根据调查结果制作统计图①和图②,请根据相关信息,解答下列问题:
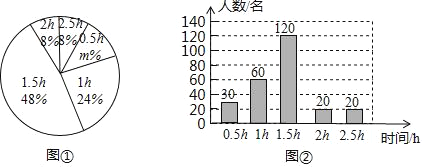
(1)本次接受随机抽样调查的中学生人数为_______,图①中m的值是_____ ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据统计数据,估计该地区250000名中学生中,每天在校体育锻炼时间大于等于1.5h的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
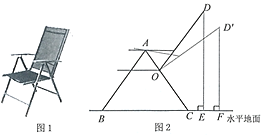
【题目】图1是小慧在“天猫双11”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,己知两支脚![]() 分米,
分米,![]() 分米,
分米,![]() 为
为![]() 上固定连接点,靠背
上固定连接点,靠背![]() 分米.档位为Ⅰ档时,
分米.档位为Ⅰ档时,![]() ,档位为Ⅱ档时,
,档位为Ⅱ档时,![]() .当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端
.当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端![]() 向后靠的水平距离(即
向后靠的水平距离(即![]() )为______分米.
)为______分米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商经销的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份冰箱每台售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(y≤12),请问有几种进货方案?
(3)三月份为了促销,该经销商决定在二月份售价的基础上,每售出一台冰箱再返还顾客现金a元,而洗衣机按每台4400元销售,这种情况下,若(2)中各方案获得的利润相同,则a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
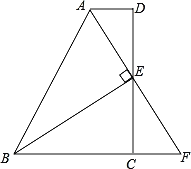
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
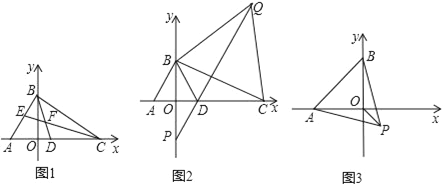
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(-3,3),B(-4,-2),C(-1,-1).
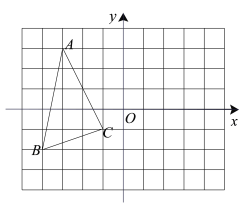
(1)在图中作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标________;
(2)在y轴上画出点P,使PA+PC最小,并直接写出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
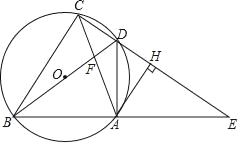
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA 交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com