
【题目】某经销商经销的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份冰箱每台售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(y≤12),请问有几种进货方案?
(3)三月份为了促销,该经销商决定在二月份售价的基础上,每售出一台冰箱再返还顾客现金a元,而洗衣机按每台4400元销售,这种情况下,若(2)中各方案获得的利润相同,则a应取何值?
【答案】(1)二月份冰箱每台售价为4000元;(2)有五种购货方案;(3)a的值为100.
【解析】
(1)设二月份冰箱每台售价为x元,则一月份冰箱每台售价为(x+500)元,根据数量=总价÷单价结合卖出相同数量的冰箱一月份的销售额为9万元而二月份的销售额只有8万元,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)根据总价=单价×数量结合预计用不多于7.6万元的资金购进这两种家电共20台,即可得出关于y的一元一次不等式,解之即可得出y的取值范围,结合y≤12及y为正整数,即可得出各进货方案;
(3)设总获利为w,购进冰箱为m台,洗衣机为(20﹣m)台,根据总利润=单台利润×购进数量,即可得出w关于m的函数关系式,由w为定值即可求出a的值.
(1)设二月份冰箱每台售价为x元,则一月份冰箱每台售价为(x+500)元,
根据题意,得:![]() =
=![]() ,
,
解得:x=4000,
经检验,x=4000是原方程的根.
答:二月份冰箱每台售价为4000元.
(2)根据题意,得:3500y+4000(20﹣y)≤76000,
解得:y≥8,
∵y≤12且y为整数,
∴y=8,9,10,11,12.
∴洗衣机的台数为:12,11,10,9,8.
∴有五种购货方案.
(3)设总获利为w,购进冰箱为m台,洗衣机为(20﹣m)台,
根据题意,得:w=(4000﹣3500﹣a)m+(4400﹣4000)(20﹣m)=(100﹣a)m+8000,
∵(2)中的各方案利润相同,
∴100﹣a=0,
∴a=100.
答:a的值为100.


科目:初中数学 来源: 题型:
【题目】为了防止水土流失,某村开展绿化荒山活动,计划经过若干年使本村绿化总面积新增360万平方米.自2014年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.问实际每年绿化面积多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1:y=kx+b(k、b为常数,且k≠0)经过A、B两点,点A在y轴上.
(1)若B点坐标为(﹣1,2).
①b= (用含有字母k的代数式表示)
②当△OAB的面积为2时,求直线l1的表达式;
(2)若B点坐标为(k﹣2b,b﹣b2),点C(﹣1,s)也在直线l1上,
①求s的值;
②如果直线l1:y=kx+b(k≠0)与直线l2:y=x交于点(x1,y1),且0<x1<2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
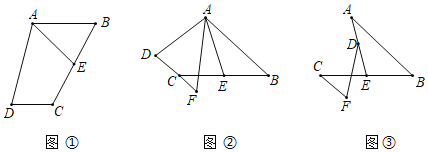
【题目】(1)问题探究:如图①,在四边形ABCD中,AB∥CD,E是BC的中点,AE是∠BAD的平分线,则线段AB,AD,DC之间的等量关系为 ;
(2)方法迁移:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,AE是∠BAF的平分线,试探究线段AB,AF,CF之间的等量关系,并证明你的结论;
(3)联想拓展:如图③,AB∥CF,E是BC的中点,点D在线段AE上,∠EDF=∠BAE,试探究线段AB,DF,CF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 两村在一条小河的同一侧,要在河边建水厂向两村供水.
两村在一条小河的同一侧,要在河边建水厂向两村供水.
(1)若要使自来水厂到两村的距离相等,厂址![]() 应选在哪个位置?
应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址![]() 应选在哪个位置?
应选在哪个位置?
(3)自来水厂建好后,在招收职工的试卷中有道题“请你在河流![]() 上找出一点
上找出一点![]() ,使
,使![]() 的值最大.”你能找到
的值最大.”你能找到![]() 点吗?请将上述
点吗?请将上述![]() 三点在下列各图分别标出,并保留尺规作图痕迹.
三点在下列各图分别标出,并保留尺规作图痕迹.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在
在![]() 的正北方向,
的正北方向,![]() 在
在![]() 的正东方向,且
的正东方向,且![]() .某一时刻,甲车从
.某一时刻,甲车从![]() 出发,以
出发,以![]() 的速度朝正东方向行驶,与此同时,乙车从
的速度朝正东方向行驶,与此同时,乙车从![]() 出发,以
出发,以![]() 的速度朝正北方向行驶.
的速度朝正北方向行驶.![]() 小时后,位于点
小时后,位于点![]() 处的观察员发现甲、乙两车之间的夹角为
处的观察员发现甲、乙两车之间的夹角为![]() ,即
,即![]() ,此时,甲、乙两人相距的距离为( )
,此时,甲、乙两人相距的距离为( )
A. 90km B. 50![]() km C. 20
km C. 20![]() km D. 100km
km D. 100km
查看答案和解析>>
科目:初中数学 来源: 题型:
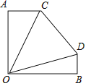
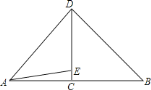
【题目】重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物![]() 的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的
的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() ,山坡
,山坡![]() 的坡度
的坡度![]() ,潘老师在
,潘老师在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() .若此时刘老师与潘老师的距离
.若此时刘老师与潘老师的距离![]() ,求建筑物
,求建筑物![]() 的高度.
的高度.![]() ,
,![]() ,
,![]() ,结果精确到
,结果精确到![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
(1)求此二次函数的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在原点处,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com