
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��l1��y��kx+b��k��bΪ��������k��0������A��B���㣬��A��y���ϣ�
��1����B����������1��2����
��b���� �����ú�����ĸk�Ĵ���ʽ��ʾ��
������OAB�����Ϊ2ʱ����ֱ��l1�ı���ʽ��
��2����B������Ϊ��k��2b��b��b2������C����1��s��Ҳ��ֱ��l1�ϣ�
����s��ֵ��
�����ֱ��l1��y��kx+b��k��0����ֱ��l2��y��x���ڵ㣨x1��y1������0��x1��2����k��ȡֵ��Χ��
���𰸡���1����2+k����y��2x+4����2����0����![]() ��
��
��������
(1)�ٰ�B(��1��2)����y=kx+b�������b��ֵ��
�ڸ��������ε�����������k��ֵ���Ӷ��ɵ�ֱ�߽���ʽ��
(2)�ٰѵ�B�͵�C���뺯������ʽ�������s��ֵ��
�ڸ�������ֱ�ߵĽ�������ĺ������ȡֵ��Χ�������k��ȡֵ��Χ��
(1)����B(��1��2)����y=kx+b��
��b=2+k��
�ʴ�Ϊ��2+k��
����S��OAB=![]() (2+k)��1=2
(2+k)��1=2
��ã�k=2��
����ֱ��l1�ı���ʽΪ��y=2x+4��
(2)����ֱ��l1��y=kx+b������B(k��2b��b��b2)�͵�C(��1��s)��
��k(k��2b)+b=b��b2����k+b=s
�����ã�(b��k)2=0��
����s=b��k=0��
����ֱ��l1��y=kx+b(k��0)��ֱ��l2��y=x���ڵ�(x1��y1)��
��kx1+b=x1
(1��k)x1=b��
��b��k=0��
��b=k��
��x1=![]()
��0��x1��2��
��![]() ��0��
��0��![]() ��2
��2
��ã�![]() ��
��
��k��ȡֵ��Χ��![]() ��
��


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB��3��AD��8����EΪBC���е㣬����AE��EF�ǡ�AEC��ƽ���ߣ���AD�ڵ�F����FD����������

A. 3B. 4C. 5D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
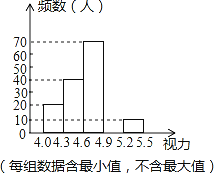
����Ŀ��ijУΪ�˽���꼶ѧ����������������꼶��ѧ��������һ���������飬�����������ݽ���ͳ�����������Ƴ�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��һ���֣�
���� | Ƶ�����ˣ� | Ƶ�� |
4.0��x��4.3 | 20 | 0.1 |
4.3��x��4.6 | 40 | 0.2 |
4.6��x��4.9 | 70 | 0.35 |
4.9��x��5.2 | a | 0.3 |
5.2��x��5.5 | 10 | b |
��1����Ƶ���ֲ����У�a=�� ����b=�� ����
��2����Ƶ���ֲ�ֱ��ͼ����������
��3����������4.6���ϣ���4.6����������������������������ռ�����������İٷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�κ��ʱ����ѧ�����ձ�������һ��������ѧ�����������㾭������һ�������������������������������ǰ����ȥǧ����������ǰ������ֱ����ǰ��ȴ��һ�ٶ�ʮ��������Ŀ�ŵ���ȡ�����������ĩ�κϣ��Ӻ��ȴ��һ�ٶ�ʮ�߲�����Ŀ�ŵ���ȡ�������������ĩ�κϣ��ʵ����Σ�

��������Ҫ����������һ��ɽ��AH�ĸ߶�����B����D���������BC��DE����˵ĸ߶���3����B��D�������1000����1��=10����1��=6�ߣ�������AH��CB��DE��ͬһƽ���ڣ��ӱ��BC����123����F�����Կ�������A�ͱ�˶���C��ͬһֱ�������ӱ��ED����127����G�����Կ�������A�ͱ�˶���E��ͬһֱ���ϣ���ɽ��AH�ĸ߶���_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ�ͣ�����ѳ�Ϊ�Ϸʳ��в�֮һ����Ҫ�����ھ�סͣ��λ���㣬ͣ����Դ�ṹ��ʧ�⣬���ij����������ȵ�.��ͼ������ʦ�ij���ǽƽ��ͣ�ŵ�ƽ��ʾ��ͼ��������ǽһ��OB��ǽMNƽ���Ҿ���Ϊ0.8�ף���֪С�������ſ�AOΪ 1.2 �ף������ŴǶȡ�AOBΪ40��ʱ�������Ƿ������ǽ����˵������.���ο����ݣ�sin 40���0.64��cos 40���0.77��tan 40���0.84��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy��������C��һ��P����C������l����������������ڵ�P��ʱ���������������������������������l�ļнǺ��������������l�ļн��������P��Ϊ����㣮�涨�����߲��ܡ���������C��������������ڡ�C��ʱ��ֻ��Բ����з���������������ڡ�C��ʱ��ֻ��Բ�ڽ��з��䣮�ر����Բ�����߲�����Ϊ������ߺͷ�����ߣ������ڡ�C�ⷴ���ʾ��ͼ��ͼ1��ʾ�����С�1=��2��

��1���ԡ�C��һ�������������߾���C��һ�η�����ʾ��ͼ��ͼ2��ʾ��P1�ǵ�1������㣮����ͼ2���������߾���C�ڶ��η����ķ�����ߺͷ����P3��
��2������O�İ뾶Ϊ1ʱ����ͼ3��
�ٵ�һ�����ڵ�һ���������ƽ����y�������ԡ�O���ⲿ������Բ�ϵ�P�����˹��߾���O����������������x��ƽ�����������������l�ļн�Ϊ___________����
���Ե�M��0��1������������������ڡ�O��˳ʱ�뷽�ϵط��䣮����1���������P1���ڶ����������P2���Դ���������8���������P8ǡ�����M�غ������1�������P1������Ϊ___________��
��3����ͼ4����M������Ϊ��0��2������M�İ뾶Ϊ1����һ�������Ե�O������������߾���M�����������������������������������P���������ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
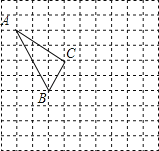
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ���������Σ�ABC�Ķ���A��C������ֱ�Ϊ����4��5��������1��3����
��1������ͼ��ʾ������ƽ��������ƽ��ֱ������ϵ����עԭ���Լ�x�ᡢy�
��2��������ABC����y��ԳƵġ�A��B��C�䣬��д����B������ꣻ
��3����P��x���ϵĶ��㣬��ͼ���ҳ�ʹ��A��BP�ܳ���Сʱ�ĵ�P��ֱ��д����P�������ǣ��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̾����ı�����·ݵ��ۼ۱�һ�·�ÿ̨����500Ԫ����֪������ͬ�����ı���һ�·ݵ����۶�Ϊ9��Ԫ�����·ݵ����۶�ֻ��8��Ԫ��
��1�����·ݱ���ÿ̨�ۼ�Ϊ����Ԫ��
��2��Ϊ��������þ����̼ƻ����·��ٹ���ϴ�»��������ۣ���֪ϴ�»�ÿ̨����Ϊ4000Ԫ������ÿ̨����Ϊ3500Ԫ��Ԥ���ò�����7.6��Ԫ���ʽ������ּҵ繲20̨�������Ϊy̨��y��12���������м��ֽ���������
��3�����·�Ϊ�˴������þ����̾����ڶ��·��ۼ۵Ļ����ϣ�ÿ�۳�һ̨�����ٷ����˿��ֽ�aԪ����ϴ�»���ÿ̨4400Ԫ���ۣ���������£�����2���и�������õ�������ͬ����aӦȡ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
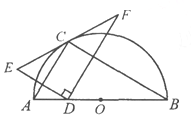
����Ŀ����ͼ����C����ABΪֱ���İ�Բ�ϣ�AB��8����CBA��30������D���߶�AB���˶�����E���D����AC�Գƣ�DF��DE�ڵ�D������EC���ӳ����ڵ�F�����н��ۣ���CE��CF�����߶�EF����СֵΪ![]() ������AD��2ʱ��EF���Բ���У�������Fǡ������BC�ϣ���AD��
������AD��2ʱ��EF���Բ���У�������Fǡ������BC�ϣ���AD��![]() ��������D�ӵ�A�˶�����Bʱ���߶�EFɨ���������
��������D�ӵ�A�˶�����Bʱ���߶�EFɨ���������![]() ��������ȷ���۵������ ��
��������ȷ���۵������ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com