
【题目】如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为![]() ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=![]() ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
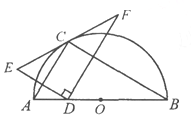
【答案】①③⑤.
【解析】
试题①连接CD,如图1所示,∵点E与点D关于AC对称,∴CE=CD,∴∠E=∠CDE,∵DF⊥DE,∴∠EDF=90°,∴∠E+∠F=90°,∠CDE+∠CDF=90°,∴∠F=∠CDF,∴CD=CF,∴CE=CD=CF,∴结论“CE=CF”正确;
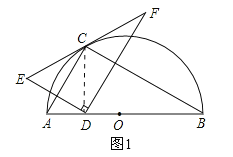
②当CD⊥AB时,如图2所示,∵AB是半圆的直径,∴∠ACB=90°,∵AB=8,∠CBA=30°,∴∠CAB=60°,AC=4,BC=![]() .∵CD⊥AB,∠CBA=30°,∴CD=
.∵CD⊥AB,∠CBA=30°,∴CD=![]() BC=
BC=![]() .根据“点到直线之间,垂线段最短”可得:点D在线段AB上运动时,CD的最小值为
.根据“点到直线之间,垂线段最短”可得:点D在线段AB上运动时,CD的最小值为![]() .∵CE=CD=CF,∴EF=2CD.∴线段EF的最小值为
.∵CE=CD=CF,∴EF=2CD.∴线段EF的最小值为![]() .∴结论“线段EF的最小值为
.∴结论“线段EF的最小值为![]() ”错误;
”错误;
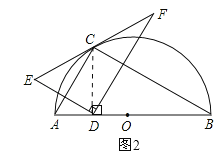
③当AD=2时,连接OC,如图3所示,∵OA=OC,∠CAB=60°,∴△OAC是等边三角形,∴CA=CO,∠ACO=60°,∵AO=4,AD=2,∴DO=2,∴AD=DO,∴∠ACD=∠OCD=30°,∵点E与点D关于AC对称,∴∠ECA=∠DCA,∴∠ECA=30°,∴∠ECO=90°,∴OC⊥EF,∵EF经过半径OC的外端,且OC⊥EF,∴EF与半圆相切,∴结论“EF与半圆相切”正确;
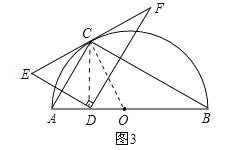
④当点F恰好落在![]() 上时,连接FB、AF,如图4所示,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴FH:FD=FC:FE,∵FC=
上时,连接FB、AF,如图4所示,∵点E与点D关于AC对称,∴ED⊥AC,∴∠AGD=90°,∴∠AGD=∠ACB,∴ED∥BC,∴△FHC∽△FDE,∴FH:FD=FC:FE,∵FC=![]() EF,∴FH=
EF,∴FH=![]() FD,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∴BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=
FD,∴FH=DH,∵DE∥BC,∴∠FHC=∠FDE=90°,∴BF=BD,∴∠FBH=∠DBH=30°,∴∠FBD=60°,∵AB是半圆的直径,∴∠AFB=90°,∴∠FAB=30°,∴FB=![]() AB=4,∴DB=4,∴AD=AB﹣DB=4,∴结论“AD=
AB=4,∴DB=4,∴AD=AB﹣DB=4,∴结论“AD=![]() ”错误;
”错误;
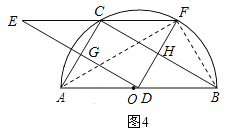
⑤∵点D与点E关于AC对称,点D与点F关于BC对称,∴当点D从点A运动到点B时,点E的运动路径AM与AB关于AC对称,点F的运动路径NB与AB关于BC对称,∴EF扫过的图形就是图5中阴影部分,∴S阴影=2S△ABC=2×![]() ACBC=ACBC=4×
ACBC=ACBC=4×![]() =
=![]() ,∴EF扫过的面积为
,∴EF扫过的面积为![]() ,∴结论“EF扫过的面积为
,∴结论“EF扫过的面积为![]() ”正确.
”正确.
故答案为:①③⑤.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1:y=kx+b(k、b为常数,且k≠0)经过A、B两点,点A在y轴上.
(1)若B点坐标为(﹣1,2).
①b= (用含有字母k的代数式表示)
②当△OAB的面积为2时,求直线l1的表达式;
(2)若B点坐标为(k﹣2b,b﹣b2),点C(﹣1,s)也在直线l1上,
①求s的值;
②如果直线l1:y=kx+b(k≠0)与直线l2:y=x交于点(x1,y1),且0<x1<2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
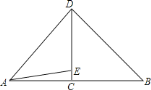
【题目】重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物![]() 的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的
的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() ,山坡
,山坡![]() 的坡度
的坡度![]() ,潘老师在
,潘老师在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() .若此时刘老师与潘老师的距离
.若此时刘老师与潘老师的距离![]() ,求建筑物
,求建筑物![]() 的高度.
的高度.![]() ,
,![]() ,
,![]() ,结果精确到
,结果精确到![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
(1)求此二次函数的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在原点处,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(-2,1),B(-3,4),C(-1,3),过点(l,0)作x轴的垂线![]() .
.
(1)作出△ABC关于直线![]() 的轴对称图形△
的轴对称图形△![]() ;
;
(2)直接写出A1(___,___),B1(___,___),C1(___,___);
(3)在△ABC内有一点P(m,n),则点P关于直线![]() 的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).
的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
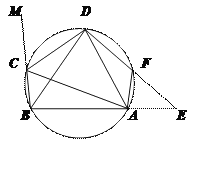
【题目】在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
⑴求证△ABD为等腰三角形.
⑵求证ACAF=DFFE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=x2﹣2mx+m2+![]() m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
(1)分别用含有m的代数式表示点A、B的坐标.
(2)判断点B能否落在y轴负半轴上,并说明理由.
(3)连结AC,设l=AC+BD,求l与m之间的函数关系式.
(4)过点A作y轴的垂线,交y轴于点P,以AP为边作正方形APMN,MN在AP上方,如图②,当正方形APMN与四边形ABCD重叠部分图形为四边形时,直接写出m的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com