
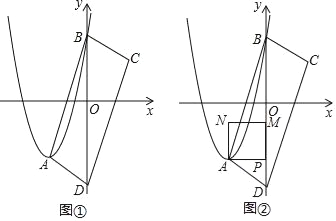
【题目】如图①,在平面直角坐标系中,抛物线y=x2﹣2mx+m2+![]() m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
(1)分别用含有m的代数式表示点A、B的坐标.
(2)判断点B能否落在y轴负半轴上,并说明理由.
(3)连结AC,设l=AC+BD,求l与m之间的函数关系式.
(4)过点A作y轴的垂线,交y轴于点P,以AP为边作正方形APMN,MN在AP上方,如图②,当正方形APMN与四边形ABCD重叠部分图形为四边形时,直接写出m的取值范围.

【答案】(1)A(m, ![]() m),(0,m2+
m),(0,m2+![]() m);(2)点B能落在y轴负半轴上;(3)l=2m2﹣
m);(2)点B能落在y轴负半轴上;(3)l=2m2﹣![]() m;(4)m<﹣1.
m;(4)m<﹣1.
【解析】试题分析:
(1)①把![]() 配方化为顶点式,可得顶点A的坐标;②在
配方化为顶点式,可得顶点A的坐标;②在![]() 中,由
中,由![]() 可得
可得![]() ,由此可得点B的坐标;
,由此可得点B的坐标;
(2)由顶点A的位置可得“![]() ”;由点B的坐标为
”;由点B的坐标为![]() 可知,若点B在
可知,若点B在![]() 轴负半轴,则有
轴负半轴,则有![]() ,两者结合可解得:
,两者结合可解得: ![]() 时,点B就在
时,点B就在![]() 轴负半轴;
轴负半轴;
(3)由题意可知: ![]() =AC+BD=2OA+OB,由点A、B的坐标可用和含“
=AC+BD=2OA+OB,由点A、B的坐标可用和含“![]() ”的代数式表达出OA、OB的长度,从而可得
”的代数式表达出OA、OB的长度,从而可得![]() 与
与![]() 间的函数关系式;
间的函数关系式;
(4)由题意可知,当AP<BP时,正方形APMN与四边形ABCD重叠部分图形为四边形时,由AP= ![]() ,BP=
,BP= ![]() 列出不等式,结合
列出不等式,结合![]() 即可求出
即可求出![]() 的取值范围;
的取值范围;
试题解析:
(1)∵把![]() 配方,得:
配方,得: ![]() ,
,
∴顶点A的坐标为![]() ;
;
∵在![]() 中,当
中,当![]() 时,
时, ![]() ;
;
∴点B的坐标为![]() ;
;
(2)点B能落在y轴负半轴上,理由如下:
由图可知顶点A![]() 在第三象限,
在第三象限,
∴![]() ,
,
∵B点的纵坐标要小于零,
∴![]() ,
,
由![]() ,得:
,得: ![]() ,
,
解得: ![]() ,
,
即当![]() 时,点B能落在
时,点B能落在![]() 轴的负半轴上;
轴的负半轴上;
(3)由点A、B关于原点的对称点分别为C、D,可得:AC=2OA,BD=2OB,
∵A的坐标为![]() ,B的坐标为
,B的坐标为![]() ,
,
∴OA= ![]() ,OB=
,OB= ![]() ,
,
∴![]() =AC+BD=2OA+2OB=
=AC+BD=2OA+2OB= ![]() ;
;
(4)由题意,当正方形APMN与四边形ABCD重叠部分图形为四边形时,AP<BP,
∵AP= ![]() ,BP=
,BP= ![]() ,
,
∴![]()
![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ,解得:
,解得: ![]() ,
,
∴当正方形APMN与四边形ABCD重叠部分图形为四边形时, ![]() 的取值范围是:
的取值范围是: ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE. 
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)计算:
(1)3·(x4)6-2(x5·x3)3+x11·x13+x20·x3·x;
(2)(-4×103)2×(-2×103)2;
(3) ![]() 100×
100×![]() 99×
99×![]() 100;
100;
(4) ![]() 2 015·(x2)2 015-(-0.125)3×29+(-0.25)2 014×42 014;
2 015·(x2)2 015-(-0.125)3×29+(-0.25)2 014×42 014;
(5)162m÷42n÷4m×43m-3n+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论
①a>0,②b>0,③c>0,④b2﹣4ac>0
其中正确的有( )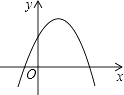
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上. 
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过70 km/h,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪 A的正前方60 m处的C点,过了5 s后,测得小汽车所在的B点与车速检测仪A之间的距离为100 m.
(1)求B,C间的距离.
(2)这辆小汽车超速了吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国逐步完善养老金保险制度,甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com