
【题目】图1是小慧在“天猫双11”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,己知两支脚![]() 分米,
分米,![]() 分米,
分米,![]() 为
为![]() 上固定连接点,靠背
上固定连接点,靠背![]() 分米.档位为Ⅰ档时,
分米.档位为Ⅰ档时,![]() ,档位为Ⅱ档时,
,档位为Ⅱ档时,![]() .当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端
.当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端![]() 向后靠的水平距离(即
向后靠的水平距离(即![]() )为______分米.
)为______分米.
【答案】2
【解析】
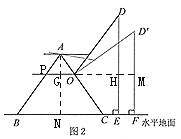
如图,作AN⊥BC,交PO于G点,延长GO,交DE于H,交D’F于M,根据等腰三角形的性质得到NC的长,故得到cos∠ABN的值,根据题意知GO∥BC,DO∥AB,可得到cos∠DOH=cos∠ABN,根据![]() 即可得到OH的长,又
即可得到OH的长,又![]() ,可得∠D’OM=∠OAG,再求出cos∠OAG=
,可得∠D’OM=∠OAG,再求出cos∠OAG=![]() 即可求出OM,故可得到EF的长.
即可求出OM,故可得到EF的长.
如图,作AN⊥BC,交PO于G点,延长GO,交DE于H,交D’F于M,
∵![]() ,
,![]() ,
,
∴BN=CN=6,AN=![]()
∴cos∠ABN=![]() ,
,
根据题意得GO∥BC,DO∥AB,
∴∠DOH=∠APG=∠ABG
∴cos∠DOH=cos∠ABN
∴cos∠DOH= ![]() =
= ![]()
∴OH=6,
由![]() ,
,
∴∠AOG+∠D’OM=90°,又∠AOG+∠OAG =90°
∴∠D’OM=∠OAG,
∵cos∠OAG=![]() =
=![]()
∴cos∠D’OM =![]() =
=![]()
∴OM=8
∴HM=2,
则EF=2,
故答案为:2.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC=3![]() ,求DE的长;
,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3![]() ,求图中阴影部分面积.
,求图中阴影部分面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2019年9月1日起,我市积极开展垃圾分类活动,市环卫局准备购买![]() 、
、![]() 两种型号的垃圾箱,通过市场调研得知:购买3个
两种型号的垃圾箱,通过市场调研得知:购买3个![]() 型垃圾箱和2个
型垃圾箱和2个![]() 型垃圾箱共需540元;购买2个
型垃圾箱共需540元;购买2个![]() 型垃圾箱比购买3个
型垃圾箱比购买3个![]() 型垃圾箱少用160元.
型垃圾箱少用160元.
(1)求每个![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱各多少元?
型垃圾箱各多少元?
(2)该市现需要购买![]() 、
、![]() 两种型号的垃圾箱共30个,设购买
两种型号的垃圾箱共30个,设购买![]() 型垃圾箱
型垃圾箱![]() 个,购买
个,购买![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱的总费用为
型垃圾箱的总费用为![]() 元,求
元,求![]() 与
与![]() 的函数表达式,如果买
的函数表达式,如果买![]() 型垃圾箱是
型垃圾箱是![]() 型垃圾箱的2倍,求出购买
型垃圾箱的2倍,求出购买![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱的总费用.
型垃圾箱的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
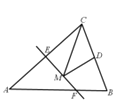
【题目】如图,等腰三角形ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
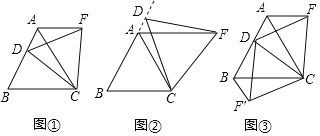
(1)操作发现:如图1,点D是等边△ABC边BA上一动点(点D与点B不重合),连结DC,以DC为边在CD上方作等边△DCF,连结AF,你能发现线段AF与BD之间的数量关系吗?证明你发现的结论.
(2)类比猜想:如图2,当动点D运动至等边△ABC边BA的延长线上时,其余条件不变,猜想:(1)中的结论是否成立,并说明理由.
(3)拓展探究:如图3.当动点D在等边△ABC边BA上运动时(点D与点B不重合),连结DC,以DC为边在CD上方和下方分别作等边△DCF和等边△DCF′,连结AF,BF′,探究:AF、BF′与AB有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
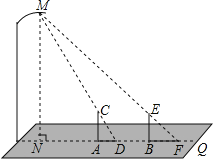
【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
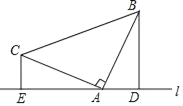
【题目】已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线l的垂线段BD、CE,垂足分别D、E.
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请画出图形,直接给出你的结论(不用证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
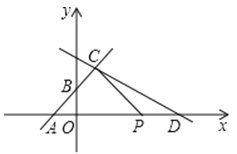
【题目】如图,在平面直角坐标系中,直线![]() 与
与 ![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 为直线
为直线 ![]() 上一点,直线
上一点,直线![]()
![]() 过点
过点![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)直线![]() 与
与 ![]() 轴交于点
轴交于点![]() ,动点
,动点 ![]() 在射线
在射线 ![]() 上从点
上从点![]() 开始以每秒 1 个单位的速度运动.设点
开始以每秒 1 个单位的速度运动.设点 ![]() 的运动时间为
的运动时间为![]() 秒;
秒;
①若![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与 ![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 ![]() 的取值范围;
的取值范围;
②是否存在 ![]() 的值,使得
的值,使得 ![]() ?若存在,请求出
?若存在,请求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com