
【题目】已知二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象交于两点A(-2,-5)和B(1,4),且二次函数图象与y轴的交点在直线y=2x+3上,求这两个函数的解析式。
【答案】y=3x+1;y=-x2+2x+3.
【解析】
试题分析:将点A(-2,-5)和B(1,4)代入一次函数y=mx+n,利用待定系数法求一次函数的解析式;然后求出一次函数y=2x+3的图象与y轴的交点是(0,3),最后将A(-2,-5)、B(1,4)和(0,3)代入二次函数y=ax2+bx+c,利用待定系数法求二次函数的解析式.
试题解析:∵一次函数y=mx+n和二次函数y=ax2+bx+c的图象相交于A(-2,-5)和B(1,4),
∴![]() ,
,
解得,![]() ,
,
∴一次函数的解析式是:y=3x+1;
又∵一次函数y=2x+3的图象与y轴的交点是(0,3),
二次函数y=ax2+bx+c的图象经过一次函数y=2x+3的图象与y轴的交点,
∴ ,解得,
,解得,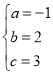 ,
,
∴二次函数的解析式:y=-x2+2x+3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
A.当a<1时,点B在⊙A外
B.当1<a<5时,点B在⊙A内
C.当a<5时,点B在⊙A内
D.当a>5时,点B在⊙A外
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别为线段AC上两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于M.说明:MB=MD,ME=MF.
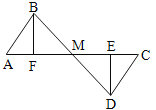
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.

(1)抛物线及直线AC的函数关系式;
(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学公司组织初三505名学生外出社会综合实践活动,现打算租用A、B 两种型号的汽车,并且每辆车上都安排1名导游,如果租用这两种型号的汽车各5辆,则刚好坐满;如果全部租用B型汽车,则需13辆汽车,且其中一辆会有2个空位,其余汽车都坐满.(注:同种型号的汽车乘客座位数相同)
(1)A、B两种型号的汽车分别有多少个乘客座位?
(2)综合考虑多种因素,最后该公司决定租用9辆汽车,问最多安排几辆B型汽车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com