
����Ŀ����ͼ����֪������y=��x2+bx+c��һֱ���ཻ��A����1��0����C��2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��

��1��������ֱ��AC�ĺ�����ϵʽ��
��2���������ߵĶԳ�����ֱ��AC�ཻ�ڵ�B��EΪֱ��AC�ϵ�����һ�㣬����E��EF��BD���������ڵ�F����B��D��E��FΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E�����ꣻ�����ܣ���˵�����ɣ�
��3����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ.
���𰸡���1��y=-x2+2x+3��y=x+1����2���ܣ���0��1������![]() ��
��![]() ����
����![]() ��
��![]() ������3��
������3��![]() ��
��
��������
�����������1�����ô���ϵ��������κ�������ʽ��һ�κ�������ʽ��
��2����Ҫ�������ۣ�������E���߶�AC��ʱ����F�ڵ�E�Ϸ�����F��x��x+3����������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·�����F��x��x-1����Ȼ�����ö��κ���ͼ���ϵ����������������õ�E�����ꣻ
��3������P��PQ��x�ύAC�ڵ�Q������C��CG��x���ڵ�G����ͼ1����Q��x��x+1������P��x��-x2+2x+3�������������ľ��빫ʽ��������߶�PQ=-x2+x+2�������ͼʾ�Լ������ε������ʽ֪S��APC=-![]() ��x-
��x-![]() ��2+
��2+![]() �������ɶ��κ�������ֵ����֪��APC����������ֵ.
�������ɶ��κ�������ֵ����֪��APC����������ֵ.
�����������1����������y=-x2+bx+c����A��-1��0����C��2��3���ã�
![]() ��
��
���![]() ��
��
��������Ϊy=-x2+2x+3
����ֱ��Ϊy=kx+n����A��-1��0����C��2��3����
![]() ��
��
���![]()
��ֱ��ACΪy=x+1��
��2���ɣ�1������2����D��1��4����B��1��2����
����E��ֱ��AC�ϣ�
��E��x��x+1����
����ͼ2������E���߶�AC��ʱ����F�ڵ�E�Ϸ���
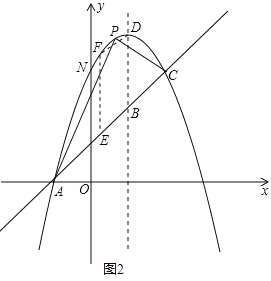
��F��x��x+3����
��F���������ϣ�
��x+3=-x2+2x+3��
��ã�x=0��x=1����ȥ��
��E��0��1����
������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·���
��F��x��x-1��
��F����������
��x-1=-x2+2x+3
���x=![]() ��x=
��x=![]()
��E��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
���ϣ����������ĵ�E������Ϊ��0��1������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3����ͼ3������P��PQ��x�ύAC�ڵ�Q����x���ڵ�H������C��CG��x���ڵ�G����Q��x��x+1������P��x��-x2+2x+3��
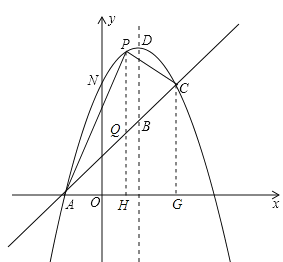
��PQ=��-x2+2x+3��-��x+1��=-x2+x+2
����S��APC=S��APQ+S��CPQ
=![]() PQ
PQ ![]() AG
AG
=![]() ��-x2+x+2����3
��-x2+x+2����3
=-![]() ��x-
��x-![]() ��2+
��2+![]()
����������ֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��в�������¼����ǣ� ��
A�����ӻ������ڲ��Ź��
B�����к���Ͱ���ĺ����������ó�һ�������ǰ���
C���ӿα���������һ���������õ���ѧ��
D������̫�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ�������
A. a2a4��a8B. a10��a5��a2C. ��a5��2��a10D. ��2a��4��8a4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y1=ax2+bx+c��һ�κ���y2=mx+n��ͼ��������A��-2��-5����B��1��4�����Ҷ��κ���ͼ����y��Ľ�����ֱ��y=2x+3�ϣ��������������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽���ⷽ��x2��4x��3=0ʱ���䷽��õ��ķ���Ϊ��������
A. (x��2)2 = 1 B. ( x��2)2 =3 C. (x��2)2 = 3 D. ( x��2)2 = 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾƽ��ֱ������ϵ�У���֪A��-2��2����B��-3��-2����C��3��-2��.

��1����ͼ�л�����ABC��
��2������ABC������ƽ��4����λ����������ƽ��2����λ���õ���A1B1C1��д����A1��B1��C1�����ꣻ
��3�����A1B1C1�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����зֽ���ʽ��ȷ���ǣ� ��
A.x3��x=x��x2��1��
B.x2��x+2=x��x��1��+2
C.x2+2x��1=��x��1��2
D.x2��1=��x+1����x��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.ƽ�Ʋ��ı�ͼ�ε���״�ʹ�С������ת��ı�ͼ�ε���״�ʹ�С
B.�ڳ����ĶԳƵ�����ͼ���У�����ԳƵ���߶ζ����Գ�����ƽ��
C.��ƽ��ֱ������ϵ�У�һ������ƽ��2����λ���������2
D.��ƽ�ƺ���תͼ���У���Ӧ����ȣ���Ӧ�߶������ƽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com