
分析 (1)方程组利用加减消元法求出解即可.
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)$\left\{\begin{array}{l}{\frac{1}{2}x+3y=-6①}\\{\frac{1}{2}x+y=2②}\end{array}\right.$
①-②得:2y=-8,
解得:y=-4,
把y=-4代入②得:x=12,
则方程组的解为$\left\{\begin{array}{l}{x=12}\\{y=-4}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{3(x-1)+1>5x-2(1-x)①}\\{5-(2x-1)<-6x②}\end{array}\right.$
∵解不等式①得:x<0,
解不等式②得:x>-$\frac{3}{2}$,
∴不等式组的解集为-$\frac{3}{2}$<x<0.
点评 本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是能根据找不等式组解集的规律找出不等式组的解集,本题也考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
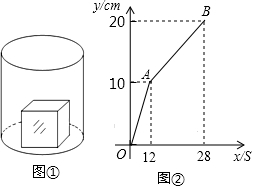 如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
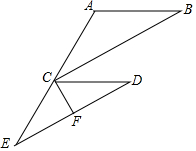 如图,AB∥CD,点E在AC上,CB平分∠ACD,∠B=30°,CF⊥DE,垂足为F,∠ECF=60°,.
如图,AB∥CD,点E在AC上,CB平分∠ACD,∠B=30°,CF⊥DE,垂足为F,∠ECF=60°,.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com