
����Ŀ����ͼ��������y=ax2+bx��3a��a��0����x�ύ�ڵ�A����1��0���͵�B����y�ύ�ڵ�C��0��2��������BC��
��1����������ߵĽ���ʽ�ͶԳ��ᣬ��д���߶�BC���е����ꣻ
��2�����߶�BC������ƽ��2����λ���ȣ�������ƽ��m����λ���ȣ�ʹ��C�Ķ�Ӧ��C1ǡ�����ڸ��������ϣ����ʱ��C1�������m��ֵ��
��3������P�Ǹ��������ϵĶ��㣬��Q�Ǹ������߶Գ����ϵĶ��㣬����P��Q��B��C�ĵ�Ϊ������ı�����ƽ���ı���ʱ�����ʱ��P�����꣮
���𰸡�
��1��
�⣺��������y=ax2+bx��3a��a��0����x�ύ�ڵ�A����1��0���͵�B����y�ύ�ڵ�C��0��2����
�� ![]() ��
��
���  ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x+2=��
x+2=�� ![]() ��x��1��2+2
��x��1��2+2 ![]() ��
��
��Գ�����x=1��
��1+��1+1��=3��
��B��������3��0����
��BC���е�����Ϊ��1.5��1��
��2��
�⣺���߶�BC������ƽ��2����λ���ȣ�������ƽ��m����λ���ȣ�ʹ��C�Ķ�Ӧ��C1ǡ�����ڸ��������ϣ�
���C1�ĺ�����Ϊ��2��
��x=��2ʱ��y=�� ![]() ������2��2+
������2��2+ ![]() ������2��+2=��
������2��+2=�� ![]() ��
��
���C1����������2���� ![]() ����
����
m=2������ ![]() ��=5
��=5 ![]()
��3��
�⣺����BCΪƽ���ı��ε�һ�ߣ�
��BC�ĺ�����IJ�Ϊ3��
�ߵ�Q�ĺ�����Ϊ1��
��P�ĺ�����Ϊ4��2��
��P���������ϣ�
��P����������3 ![]() ��
��
��P1��4����3 ![]() ����P2����2����3
����P2����2����3 ![]() ����
����
����BCΪƽ���ı��εĶԽ��ߣ�
��BC��PQ����ƽ�֣�
�ߵ�Q�ĺ�����Ϊ1��BC���е�����Ϊ��1.5��1����
��P��ĺ�����Ϊ1.5+��1.5��1��=2��
��P���������� ![]() ��22+
��22+ ![]() ��2+2=2��
��2+2=2��
��P3��2��2����
������������P��������P1��4����3 ![]() ����P2����2����3
����P2����2����3 ![]() ����P3��2��2��
����P3��2��2��
����������1���ѵ�A����1��0���͵�C��0��2��������������������߿ɵ�a��b��ֵ�������õ��������ߵĽ���ʽ�ͶԳ��ᣬ�������B�����꣬�����е����깫ʽ����߶�BC���е����꼴�ɣ���2������ƽ�Ƶ����ʿ�֪����C�Ķ�Ӧ��C1�ĺ�����Ϊ��2���ٴ��������߿����C1�����꣬��һ���õ�m��ֵ����3��B��CΪ���㣬�ɷ�BCΪƽ���ı��ε�һ���Խ����������̽�ֵõ���P�����꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ�������ABCD�У���B=60�㣬P��Qͬʱ��B��������ÿ��1����λ���ȷֱ���B��A��D��C��B��C��D�����˶�������ʱֹͣ�����˶�ʱ��Ϊt���룩����BPQ�����ΪS��ƽ����λ����S��t�ĺ���ͼ����ͼ2�������н��۴�����ǣ� ��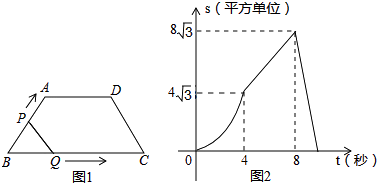
A.��t=4��ʱ��S=4 ![]()
B.AD=4
C.��4��t��8ʱ��S=2 ![]() t
t
D.��t=9��ʱ��BPƽ������ABCD�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
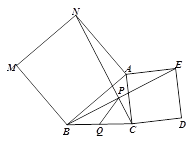
����Ŀ��̽������ͼ���ֱ��ԡ�ABC������AB��ACΪ��������������ABMN��������ACDE��CN��BE���ڵ�P. ��֤����ANC = ��ABE.
Ӧ�ã�Q���߶�BC���е㣬����PQ. ��BC = 6����PQ = ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ҵ������һ��������Ŀ��Ϊ�˽�Լ��Դ����������������ҵ��������A��B�����ͺŵ���ˮ�����豸��10̨������������±���
A�� | B�� | |
�۸���Ԫ/̨�� | 15 | 12 |
����ˮ������������/�£� | 250 | 200 |
��Ԥ�㣬��ҵ���֧��136��Ԫ�����豸����Ҫ���´�����ˮ����������2150�֣�
��1������ҵ���ļ��ֹ�����
��2�����ַ�����ʡǮ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڿ�չ�����������������塱�Ļ��ij����ƻ�����A��B�������繲100�ã���֪A������ÿ��30Ԫ��B������ÿ��90Ԫ��
��1���蹺��A������x�ã�����A��B����������ܷ���ΪyԪ������д��y��x֮��ĺ�����ϵʽ����Ҫ��д���Ա���x��ȡֵ��Χ����
��2���������A��B����������ܷ��ò�����7560Ԫ����B������Ŀ���������A�����������3������ô���ļ��ֹ�������ķ�����
��3���ӽ�Լ��֧�ĽǶȿ��ǣ�����Ϊ�������ַ��������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��ͼ����ͼ��ʾ����|a��b+c|+|2a+b|=�� �� 
A.a+b
B.a��2b
C.a��b
D.3a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�ڷ���������y= ![]() ��k��0����ͼ���ϣ�AC��x�ᣬBD��x�ᣬ����C��D�ֱ���x��������������ϣ�CD=k����֪AB=2AC��E��AB���е㣬�ҡ�BCE������ǡ�ADE�������2������k��ֵ�� ��
��k��0����ͼ���ϣ�AC��x�ᣬBD��x�ᣬ����C��D�ֱ���x��������������ϣ�CD=k����֪AB=2AC��E��AB���е㣬�ҡ�BCE������ǡ�ADE�������2������k��ֵ�� �� 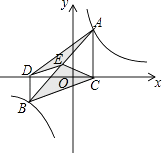
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O���ӳ�CB����F��ʹCF=CA������AF����ACF��ƽ���߷ֱ�AF��AB��BD�ڵ�E��N��M������EO�� 
��1����֪BD= ![]() ����������ABCD�ı߳���
����������ABCD�ı߳���
��2�������߶�EM��CN��������ϵ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=x2+bx+c��A��B��C���㣬��A�������ǣ�3��0������C�������ǣ�0����3��������P���������ϣ�
��1��b= �� c= �� ��B������Ϊ����ֱ����д�����
��2���Ƿ���ڵ�P��ʹ�á�ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱy���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF�ij������ʱ�������P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com