
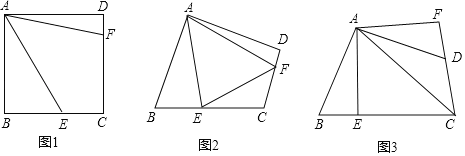
【题目】(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD.
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
(3)如图3,四边形ABCD中,∠BAD≠90°,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F,若BC=8,CD=3,则CE= .(不需证明)
【答案】(1)详见解析;(2)∠BAD=2∠EAF,理由详见解析;(3)CE=5.5.
【解析】试题分析:(1)将△ABE绕点A旋转使得AB与AD重合,然后证明△AFG≌△AFE,再利用全等三角形对应的边相等的性质不难证明;(2)首先延长CB至M,使BM=DF,连接AM,构造△ABM≌△ADF,再证明△FAE≌△MAE,最后将相等的边进行转化整理即可证明.
试题解析:
(1)证明:把△ABE绕点A逆时针旋转90°至△ADG,如图1所示:

则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BAE=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△FAE中,  , ,
, ,
∴△AFG≌△AFE(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF.
(2)∠BAD=2∠EAF.理由如下:
如图2所示,延长CB至M,使BM=DF,连接AM,

∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,  ,
,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,  ,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
(3)CE=5.5


科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1= ![]() =
= ![]() ×(1﹣
×(1﹣ ![]() );
);
第2个等式:a2= ![]() =
= ![]() ×(
×( ![]() ﹣
﹣ ![]() );
);
第3个等式:a3= ![]() =
= ![]() ×(
×( ![]() ﹣
﹣ ![]() );
);
第4个等式:a4= ![]() =
= ![]() ×(
×( ![]() ﹣
﹣ ![]() );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5=;
(2)用含有n的代数式表示第n个等式:an==(n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.

(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
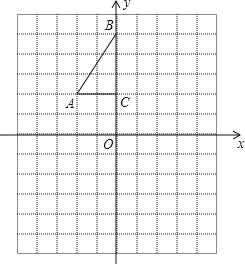
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△AˊBD.
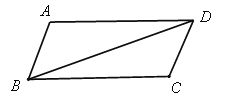
(1)利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法);
(2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O在直线AB上,点A1 , A2 , A3 , …在射线OA上,点B1 , B2 , B3 , …在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,以每秒1个单位长度的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动,即从OA1B1B2→A2…按此规律,则动点M到达A10点处所需时间为( )秒.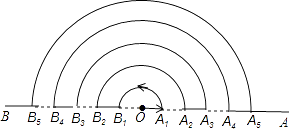
A.10+55π
B.20+55π
C.10+110π
D.20+110π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com