【题目】为了倡导绿色出行，某市政府2016年投资了320万元，首期建成120个公共自行车站点，配置2500辆公共自行车，2017年又投资了104万元新建了40个公共自行车站点，配置800辆公共自行车.
（1）请问每个站点的造价和公共自行车的单价分别是多少万元？
（2）若到2020年该市政府将再建造
个新公共自行车站点和配置
辆公共自行车，并且公共自行车数量不超过新公共自行车站点数量的23倍，并且再建造的新公共自行车站点不超过102个，市政府共有几种选择方案，哪种方案市政府投入的资金最少？（注：从2016年起至2020年，每个站点的造价和公共自行车的单价每年都保持不变）
【答案】（1）每个站点的造价1万元，公共自行车的单价0.08万元；
（2）市政府共有3种选择方案，第一种方案市政府投入的资金最，资金为284万元．
【解析】试题分析：（1）设每个站点的造价
万元，公共自行车的单价
万元，根据题意列出方程组求出即可；
（2）根据题意列出不等式组即可得.
试题解析：（1）设每个站点的造价万元，公共自行车的单价万元，
根据题意，得
，
解这个方程组，得
，
答：每个站点的造价1万元，公共自行车的单价0.08万元．
（2）根据题意可得
，解得
，
∵
为整数，
∴=100或=101或=102，
∴共有3种方案：
第一种方案：建造100个新公共自行车站点，配置2300辆公共自行车；资金为：
（万元）
第二种方案：建造101个新公共自行车站点，配置2299辆公共自行车；资金为：
（万元）
第三种方案：建造102个新公共自行车站点，配置2298辆公共自行车；资金为：
（万元）
∴第一种方案市政府投入的资金最少 ，
答：市政府共有3种选择方案，第一种方案市政府投入的资金最，资金为284万元．
科目：初中数学 来源： 题型：
【题目】(12分)
(1) 填空：
(a－b)(a＋b)＝________；
(a－b)(a2＋ab＋b2)＝________；
(a－b)(a3＋a2b＋ab2＋b3)＝________．
(2) 猜想：
(a－b)(an－1＋an－2b＋…＋abn－2＋bn－1)＝________ (其中n为正整数，且n≥2)．
(3) 利用(2)猜想的结论计算： 29－28＋27－…＋23－22＋2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了了解学生家长对孩子用手机的态度问题，随机抽取了100名家长进行问卷调查，每位学生家长只有一份问卷，且每份问卷仅表明一种态度（这100名家长的问卷真实有效），将这100份问卷进行回收整理后，绘制了如下两幅不完整的统计图．
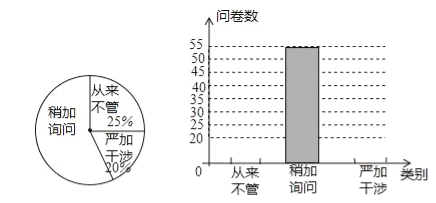
（1）“从来不管”的问卷有 份，在扇形图中“严加干涉”的问卷对应的圆心角为 ．
（2）请把条形图补充完整．
（3）若该校共有学生2000名，请估计该校对手机问题“严加干涉”的家长有多少人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小红同学要测量A、C两地的距离，但A、C之间有一水池，不能直接测量，于是她在A、C同一水平面上选取了一点B，点B可直接到达A、C两地．她测量得到AB=80米，BC=20米，∠ABC=120°．请你帮助小红同学求出A、C两点之间的距离．（参考数据
≈4.5， 
≈4.6）
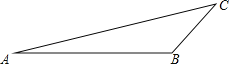
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二孩子政策的落实引起了全社会的关注，某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度，在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查，调查分别为非常赞同、赞同、无所谓、不赞同等四种态度，现将调查统计结果制成了如图两幅统计图，请结合两幅统计图，回答下列问题：
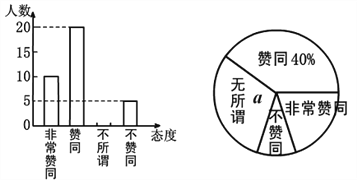
（1）在这次问卷调查中一共抽取了__________名学生，a=________%；
（2）请补全条形统计图；
（3）持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度；
（4）若该校有3000名学生，请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个样本有50个数据，其中最大值是208，最小值是169，最大值与最小值的差是______；如果取组距为5，那么这组数据应分成______组，第一组的起点为________，第二组与第一组的分点为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com