
【题目】某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查,每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如下两幅不完整的统计图.
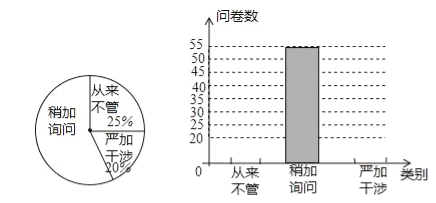
(1)“从来不管”的问卷有 份,在扇形图中“严加干涉”的问卷对应的圆心角为 .
(2)请把条形图补充完整.
(3)若该校共有学生2000名,请估计该校对手机问题“严加干涉”的家长有多少人.
【答案】(1)25,72°;(2)详见解析;(3)400.
【解析】
试题分析:(1)用100乘以问卷数“从来不管”所占百分比即可;用“严加干涉”部分占问卷总数的百分比乘以360°即可;(2)由(1)知“从来不管”的问卷数,再将问卷总数减去其余两个类别数量可得“严加干涉”的数量,进而补全条形统计图;(3)用“严加干涉”部分所占的百分比的乘以2000即可得到结果.
试题解析:(1)“从来不管”的问卷有100×25%=25(份),
在扇形图中“严加干涉”的问卷对应的圆心角为:360°×20%=72°,
(2)由(1)知,“从来不管”的问卷有25份,则“严加干涉”的问卷有100﹣25﹣55=20(份),
补全条形图如图:
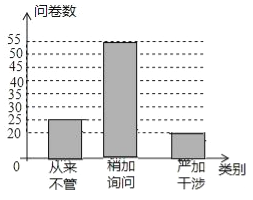
(3)2000×20%=400(人),
答:估计该校对手机问题“严加干涉”的家长有400人.


科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解九年级学生1000米跑步的训练情况,现对该年级某班学生进行了1000米跑步摸底测试,测试结果如下表所示:
得分/分 | 80 | 85 | 90 | 95 | 100 |
人数/人 | 3 | 5 | 12 | 18 | 7 |
则测试成绩的中位数和众数分别为( )
A. 90分,90分 B. 90分,95分 C. 95分,95分 D. 95分,100分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造![]() 个新公共自行车站点和配置
个新公共自行车站点和配置![]() 辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?(注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
(1)平行四边形的对角线互相平分;(2)矩形的对角线相等;(3)菱形的对角线互相垂直平分;(4)正方形的对角线相等且互相垂直平分.其中,真命题的个数是( )
A. 2B. 3C. 4D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 (x+3)(x-2)=x2+ax+b , 则a、b的值分别是( )
A.a=-1,b=-6
B.a=1,b=-6
C.a=-1,b=6
D.a=1,b=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
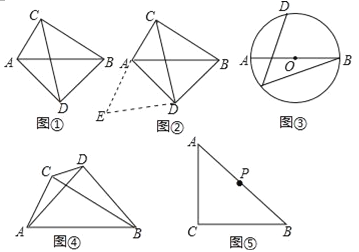
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
简单应用:
(1)在图①中,若AC=![]() ,BC=
,BC=![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙上,![]() ,若AB=13,BC=12,求CD的长.
,若AB=13,BC=12,求CD的长.
拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com