
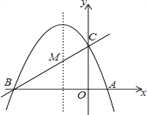
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【答案】(1)y=x+3;y=-x2-2x+3;(2)M的坐标为(-1,2);(3)P的坐标为(-1,-2)或(-1,4)或(-1, ![]() ) 或(-1,
) 或(-1, ![]() ).
).
【解析】试题分析:(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
试题解析:(1)依题意得: 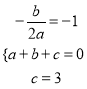 ,
,
解之得: 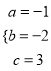 ,
,
∴抛物线解析式为y=-x2-2x+3
∵对称轴为x=-1,且抛物线经过A(1,0),
∴把B(-3,0)、C(0,3)分别代入直线y=mx+n,
得![]() ,
,
解之得: ![]() ,
,
∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2,
∴M(-1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2);
(3)设P(-1,t),
又∵B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,
①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2-6t+10解之得:t=-2;
②若点C为直角顶点,则BC2+PC2=PB2即:18+t2-6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2-6t+10=18解之得:t1=![]() ,t2=
,t2=![]() ;
;
综上所述P的坐标为(-1,-2)或(-1,4)或(-1, ![]() ) 或(-1,
) 或(-1, ![]() ).
).



科目:初中数学 来源: 题型:
【题目】为了了解某校七年级400名学生的体重情况,从中抽取50名学生进行统计分析,在这个问题中,总体是指( )。
A.400
B.被抽取的50名学生
C.400名学生的体重
D.被抽取的50名学生的体重
查看答案和解析>>
科目:初中数学 来源: 题型:
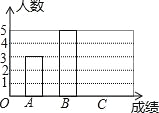
【题目】寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
编号 | 成绩 | 编号 | 成绩 |
① | B | ⑥ | A |
② | A | ⑦ | B |
③ | B | ⑧ | C |
④ | B | ⑨ | B |
⑤ | C | ⑩ | A |
根据统计图表信息解答下列问题:
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值分别为( )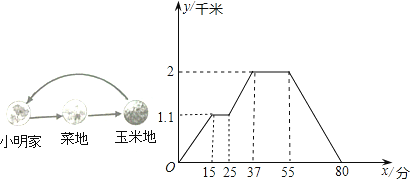
A.1.1,8
B.0.9,3
C.1.1,12
D.0.9,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图5—18所示,在ΔABC中,AD平分∠BAC,且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是 ( )
A.70°
B.80°
C.100°
D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com