【题目】如图，若长方形APHM,BNHP,CQHN的面积分别为7、4、6，求阴影部分的面积是多少？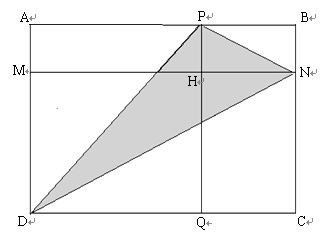
【答案】解：设四边形MHQD的面积为x，
∵长方形APHM，BNHP，CQHN的面积分别为7、4、6，
∴7：4=x：6，
x=10.5，
∴四边形ABCD的面积为：4+7+6+10.5=27.5，
S△PDN=27.5-S△ADP-S△PBN-S△DNC=27.5-1/2（4+7+10.5+6+10.5）=8.5。
【解析】根据已知及长方形APHM,BNHP,CQHN的面积，得出长方形APHM的面积：长方形BNHP的面积=长方形MHQD的面积：长方形CQHN的面积，即可求出长方形MHQD的面积，就可求出四边形ABCD的面积，然后根据S△PDN=27.5-S△ADP-S△PBN-S△DNC ， 就可求出阴影部分的面积。
科目：初中数学 来源： 题型：
【题目】某部队将在指定山区进行军事演习，为了使道路便于部队重型车辆通过，部队工兵连接到抢修一段长3600米道路的任务，按原计划完成总任务的
后，为了让道路尽快投入使用，工兵连将工作效率提高了50%，一共用了10小时完成任务．
（1）按原计划完成总任务的
时，已抢修道路 米；
（2）求原计划每小时抢修道路多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个口袋中有10个除颜色外均相同的球，其中红球3个，白球7个，从中任意取一个，那么（ ）
A.一定摸到白球B.一定摸不到白球
C.可能摸到红球D.一定摸不到红球
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，按照一定规律写出了如下各点坐标：点A1（2，2），A2（3，5），A3（4，10），A4（5，17），…请你仔细观察，按照此规律点A10的坐标应为.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形OABC的边OA在x轴上，O与原点重合，OA=1，OC=2，点D的坐标为（2，0），则直线BD的函数表达式为（ ）.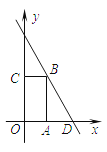
A.y=-x+2
B.y=-2x+4
C.y=-x+3
D.y=2x+4
查看答案和解析>>
科目：初中数学 来源： 题型：
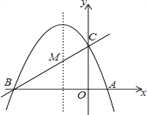
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为抛物线的对称轴x=-1上的一个动点，求使△BPC为直角三角形的点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面数据是截至2010年费尔兹奖得主获奖时的年龄：
29 39 35 33 39 28 33 35 31 31 37 32 38
36 31 39 32 38 37 34 29 34 38 32 35 36
33 29 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 40 31 38 38 40 40 37
小果、小冻、小甜将数据整理，分别按组距是2，5，10进行分组，列出频数分布表，画出频数分布直方图，如下
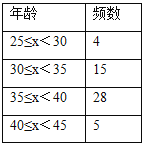
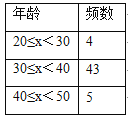
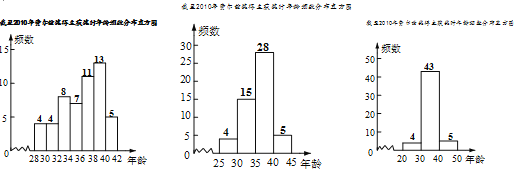
根据以上材料回答问题：
小果、小冻、小甜三人中，比较哪一位同学分组能更好的说明费尔兹奖得主获奖时的年龄分布，并简要说明其他两位同学分组的不足之处.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com