【题目】关于二次函数y=ax2+bx+c的图象有下列命题：
①当c=0时，函数的图象经过原点；
②当c＞0，且函数的图象开口向下时，方程ax2+bx+c=0必有两个不相等的实根；
③函数图象最高点的纵坐标是
；
④当b=0时，函数的图象关于y轴对称．
其中正确命题的个数是（ ）
A.1个 B.2个 C.3个 D.4个
科目：初中数学 来源： 题型：
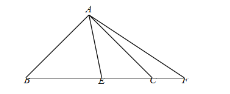
【题目】综合实践课上，某小组同学将直角三角形纸片放到横线纸上（所有横线都平行，且相邻两条平行线的距离为1），使直角三角形纸片的顶点恰巧在横线上，发现这样能求出三角形的边长．
（1）如图1，已知等腰直角三角形纸片△ABC，∠ACB=90°，AC=BC，同学们通过构造直角三角形的办法求出三角形三边的长，则AB=__________；
（2）如图2，已知直角三角形纸片△DEF，∠DEF=90°，EF=2DE，求出DF的长；
（3）在（2）的条件下，若橫格纸上过点E的横线与DF相交于点G，直接写出EG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC，∠B＝30°，O是BC上一点，以点O为圆心，OB长为半径作圆，恰好经过点A，并与BC交于点D．
（1）求证：CA是⊙O的切线．
（2）若AB＝2
，求图中阴影部分的面积（结果保留π）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，港口B位于港口A的南偏东
方向，灯塔C恰好在AB的中点处，一艘海轮位于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行
km，到达E处，测得灯塔C在北偏东
方向上．这时，E处距离港口A有多远？（参考数据： 
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．
（1）将△ABC向右移平2个单位长度，作出平移后的△A1B1C1，并写出△A1B1C1各顶点的坐标；
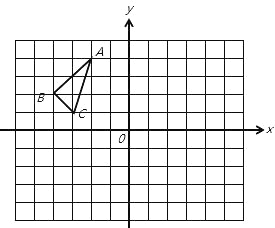
（2）若将△ABC绕点（-1，0）顺时针旋转180°后得到△A2B2C2，并写出△A2B2C2各顶点的坐标；
（3）求出三角形ABC的面积
查看答案和解析>>
科目：初中数学 来源： 题型：
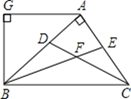
【题目】如图，AB⊥AC，CD、BE分别是△ABC的角平分线，AG∥BC，AG⊥BG，下列结论：①∠BAG=2∠ABF；②BA平分∠CBG；③∠ABG=∠ACB；④∠CFB=135°．其中正确的结论是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图，在正方形 ABCD 中，∠FAG=45°，请直接写出 DG，BF 与FG 的数量关系，不需要证明．
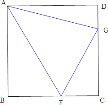
（2）如图，在 Rt△ABC 中，∠BAC=90°，AB=AC，E，F 分别是 BC 上两点，∠EAF=45°，
①写出 BE，CF，EF 之间的数量关系，并证明．
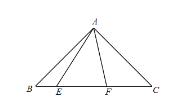
②若将（2）中的△AEF 绕点 A 旋转至如图所示的位置，上述结论是否仍然成立？ 若不成立，直接写出新的结论 ，无需证明．
（3）如图，△AEF 中∠EAF=45°，AG⊥EF 于 G，且GF=2，GE=3，则 
= ．
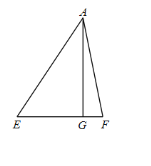
查看答案和解析>>
科目：初中数学 来源： 题型：
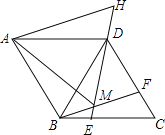
【题目】如图，在菱形ABCD中，AB=BD，点E、F分别在BC、CD上，且BE=CF，连接BF、DE交于点M，延长ED到H使DH=BM，连接AM，AH，则以下四个结论：
①△BDF≌△DCE；②∠BMD=120°；③△AMH是等边三角形；④S四边形ABCD= 
AM2．
其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知反比例函数
（k为常数，k≠0）的图象经过点A（2，3）．
（1）求这个函数的解析式；
（2）判断点B（-1，6），C（3，2）是否在这个函数的图象上，并说明理由；
（3）当-3＜x＜-1时，求y的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
