【题目】△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．

（1）将△ABC向右移平2个单位长度，作出平移后的△A1B1C1，并写出△A1B1C1各顶点的坐标；

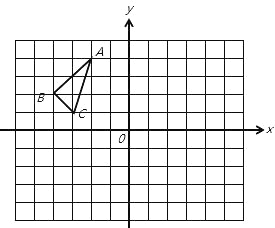
（2）若将△ABC绕点（-1，0）顺时针旋转180°后得到△A2B2C2，并写出△A2B2C2各顶点的坐标；

（3）求出三角形ABC的面积

参考答案：

【答案】（1）A1（0，4），B1（-2，2），C1（-1，1）（2）A2（0，-4），B2（2，-2），C2（1，-1）（3）2

【解析】试题分析：

（1）先在坐标系描出平移后的A1、B1、C1，顺次连接这三点即可得到所求△A1B1C1，再写出A1、B1、C1三点的坐标即可；

（2）设点（-1，0）为点D，连接AD并延长至A2，使DA2=DA即可得到A2点，同法作出B2、C2，顺次连接三点即可得到△A2B2C2，再写出三点的坐标即可；

（3）如图2，由S△ABC=S矩形ADEF-S△ADB-S△BEC-S△ACF即可求出△ABC的面积.

试题解析：

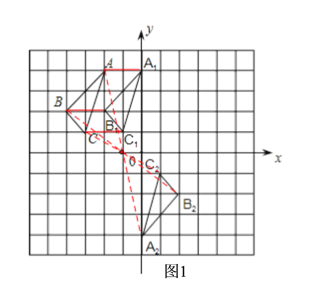
（1）如图1，图中△A1B1C1为所求三角形；三点的坐标分别为：A1（0，4），B1（-2，2），C1（-1，1）；

（2）如图1，图中△A2B2C2为所求三角形；三点的坐标分别为：A2（0，-4），B2（2，-2），C2（1，-1）；

（3）如图2，S△ABC=S矩形ADEF-S△ADB-S△BEC-S△ACF=.

关闭