
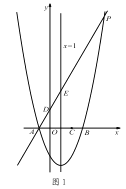
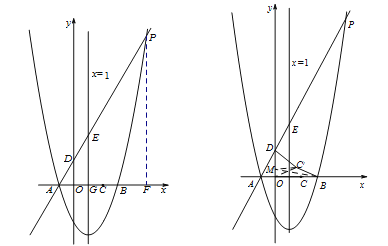
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
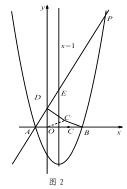
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
【答案】(1)B(3,0);抛物线的表达式为:y=![]() x2-x-
x2-x-![]() ;(2)E(1,6);(3)C′B+
;(2)E(1,6);(3)C′B+![]() C′D的最小值为
C′D的最小值为![]() .
.
【解析】试题分析:(1)由抛物线的对称轴和过点A ,即可得到抛物线的解析式,令y=0,解方程可得B的坐标;
(2)过点P作PF⊥x轴,垂足为F.由平行线分线段弄成比例定理可得![]() =
=![]() =
=![]() =
=![]() ,从而求出E的坐标;
,从而求出E的坐标;
(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,得到D(0,3).
如图,取点M(0, ![]() ),连接MC′、BM.则可求出OM,BM的长,得到△MOC′∽△C′OD.进而得到MC′=
),连接MC′、BM.则可求出OM,BM的长,得到△MOC′∽△C′OD.进而得到MC′=![]() C′D,由C′B+
C′D,由C′B+![]() C′D=C′B+MC′≥BF可得到结论.
C′D=C′B+MC′≥BF可得到结论.
试题解析:解:(1)∵抛物线y=![]() x2+bx+c的对称轴为直线x=1,∴-
x2+bx+c的对称轴为直线x=1,∴-![]() =1,∴b=-1.
=1,∴b=-1.
∵抛物线过点A(-1,0),∴![]() -b+c=0,解得:c=-
-b+c=0,解得:c=-![]() ,
,
即:抛物线的表达式为:y=![]() x2-x-
x2-x-![]() .
.
令y=0,则![]() x2-x-
x2-x-![]() =0,解得:x1=-1,x2=3,即B(3,0);
=0,解得:x1=-1,x2=3,即B(3,0);
(2)过点P作PF⊥x轴,垂足为F.
∵EG∥PF,AE:EP=1:4,∴![]() =
=![]() =
=![]() =
=![]() .
.
又∵AG=2,∴AF=10,∴F(9,0).
当x=9时,y=30,即P(9,30),PF=30,∴EG=6,∴E(1,6).
(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,则D(0,3).
∵原点O与点C关于该对称轴成轴对称,∴EG=6,∴C(2,0),∴OC′=OC=2.
如图,取点M(0, ![]() ),连接MC′、BM.则OM=
),连接MC′、BM.则OM=![]() ,BM=
,BM=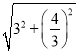 =
=![]() .
.
∵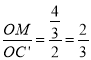 ,
, ![]() ,且∠DOC′=∠C′OD,∴△MOC′∽△C′OD.∴
,且∠DOC′=∠C′OD,∴△MOC′∽△C′OD.∴![]() ,∴MC′=
,∴MC′=![]() C′D,∴C′B+
C′D,∴C′B+![]() C′D=C′B+MC′≥BM=
C′D=C′B+MC′≥BM=![]() ,∴C′B+
,∴C′B+![]() C′D的最小值为
C′D的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】某市教育局为了了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图.请你根据图中提供的信息,回答下列问题:

(1)扇形统计图中a的值为 ;
(2)补全频数分布直方图;
(3)在这次抽样调查中,众数是 天,中位数是 天;
(4)请你估计该市初二学生每学期参加综合实践活动的平均天数约是多少?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
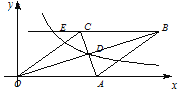
【题目】如图,在直角坐标系中,四边形 OABC 为菱形,对角线 OB、AC 相交于 D 点,已知 A点的坐标为(10,0),双曲线 y=![]() ( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=
( x>0 )经过 D 点,交 BC 的延长线于 E 点,且 OBAC=120(OB>AC),有下列四个结论:①双曲线的解析式为y=![]() (x>0);②E 点的坐标是(4,6);③sin∠COA=
(x>0);②E 点的坐标是(4,6);③sin∠COA=![]() ;④EC=
;④EC=![]() ;⑤AC+OB=8
;⑤AC+OB=8![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费”两部分组成.为了鼓励市民节约用水, 其中城市供水费按阶梯式计费:一个月用水 10 吨以内(包括 10 吨)的用户,每吨收 1.5 元;一个月用水超过 10 吨的用户,10 吨水仍按每吨 1.5 元收费,超过 10 吨的部分,按每吨 2 元收费.另外污水处理费按每吨 0.65 元收取.
(1)某居民 5 月份用水 8 吨,应交水费多少元?
(2)某居民 6 月份用水 12 吨,应交水费多少元?
(3)若某户某月用水 x 吨,请你用含有 x 的代数式表示该月应交的水费
查看答案和解析>>
科目:初中数学 来源: 题型:
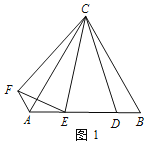
【题目】【操作发现】如图 1,△ABC 为等边三角形,点 D 为 AB 边上的一点,∠DCE=30°,将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF,连接 AF、EF. 请直接 写出下列结果:
① ∠EAF的度数为__________;
② DE与EF之间的数量关系为__________;
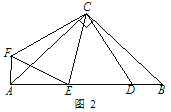
【类比探究】如图 2,△ABC 为等腰直角三角形,∠ACB=90°,点 D 为 AB 边上的一点∠DCE=45°,将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF,连接 AF、EF.
①则∠EAF的度数为__________;
② 线段 AE,ED,DB 之间有什么数量关系?请说明理由;
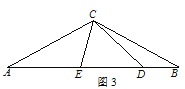
【实际应用】如图 3,△ABC 是一个三角形的余料.小张同学量得∠ACB=120°,AC=BC, 他在边 BC 上取了 D、E 两点,并量得∠BCD=15°、∠DCE=60°,这样 CD、CE 将△
ABC 分成三个小三角形,请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示是一枚质地均匀的骰子.骰子有六个面并分别代表数字1,2,3,4,5,6.如图2,正六边形ABCDEF的顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子向上的一面上的点数是几,就沿正六边形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落到圈F……
设游戏者从圈A起跳.
(1)小明随机掷一次骰子,求落回到圈A的概率P1;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率P2,并指出他与小明落回到圈A的可能性一样吗?
 图1
图1 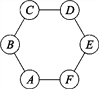 图2
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙两座仓库分别有农用车![]() 辆和
辆和![]() 辆,现需要调往
辆,现需要调往![]() 县
县![]() 辆, 调往
辆, 调往![]() 县
县![]() 辆,已知从甲仓库调运一辆农用车到
辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从乙仓库调运一辆农用车到
元,从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从甲仓库调往
元,从甲仓库调往![]() 县农用车
县农用车![]() 辆.
辆.
![]() 甲仓库调往
甲仓库调往![]() 县农用车____ 辆,乙仓库调往
县农用车____ 辆,乙仓库调往![]() 县农用车 _辆、乙仓库调往B县农用车____ 辆(用含
县农用车 _辆、乙仓库调往B县农用车____ 辆(用含![]() 的代数式表示);
的代数式表示);
![]() 写出公司从甲、乙两座仓库调农用车到
写出公司从甲、乙两座仓库调农用车到![]() 、
、![]() 两县所需要的总运费(用含
两县所需要的总运费(用含![]() 的代数式表示);
的代数式表示);
![]() 在
在![]() 的基础上,求当总运费是
的基础上,求当总运费是元时,从甲仓库调往
![]() 县农用车多少辆?
县农用车多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com