
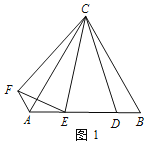
【题目】【操作发现】如图 1,△ABC 为等边三角形,点 D 为 AB 边上的一点,∠DCE=30°,将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF,连接 AF、EF. 请直接 写出下列结果:
① ∠EAF的度数为__________;
② DE与EF之间的数量关系为__________;
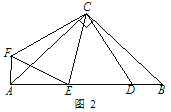
【类比探究】如图 2,△ABC 为等腰直角三角形,∠ACB=90°,点 D 为 AB 边上的一点∠DCE=45°,将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF,连接 AF、EF.
①则∠EAF的度数为__________;
② 线段 AE,ED,DB 之间有什么数量关系?请说明理由;
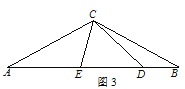
【实际应用】如图 3,△ABC 是一个三角形的余料.小张同学量得∠ACB=120°,AC=BC, 他在边 BC 上取了 D、E 两点,并量得∠BCD=15°、∠DCE=60°,这样 CD、CE 将△
ABC 分成三个小三角形,请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
【答案】 120° DE=EF 90°
【解析】试题分析:(1)①由等边三角形的性质得出AC=BC,∠BAC=∠B=60°,求出∠ACF=∠BCD,证明△ACF≌△BCD,得出∠CAF=∠B=60°,求出∠EAF=∠BAC+∠CAF=120°;
②证出∠DCE=∠FCE,由SAS证明△DCE≌△FCE,得出DE=EF即可;
(2)①由等腰直角三角形的性质得出AC=BC,∠BAC=∠B=45°,证出∠ACF=∠BCD,由SAS证明△ACF≌△BCD,得出∠CAF=∠B=45°,AF=DB,求出∠EAF=∠BAC+∠CAF=90°;
②证出∠DCE=∠FCE,由SAS证明△DCE≌△FCE,得出DE=EF;在Rt△AEF中,由勾股定理得出AE2+AF2=EF2,即可得出结论.
(3)把△BCD绕点C顺时针旋转120°得到△ACF,则可得△ACF≌△BCD,△FCE≌△DEC,得到AF=BD,EF=ED,△AEF是含30°角的直角三角形,S△BCD:S△DCE:S△ACE=BD:ED:AE= AF:EF:AE,即可得到答案.
试题解析:解:(1)①∵△ABC是等边三角形,∴AC=BC,∠BAC=∠B=60°.∵∠DCF=60°,∴∠ACF=∠BCD.在△ACF和△BCD中, 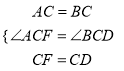 ,∴△ACF≌△BCD(SAS),∴∠CAF=∠B=60°,∴∠EAF=∠BAC+∠CAF=120°;
,∴△ACF≌△BCD(SAS),∴∠CAF=∠B=60°,∴∠EAF=∠BAC+∠CAF=120°;
②DE=EF.理由如下:
∵∠DCF=60°,∠DCE=30°,∴∠FCE=60°﹣30°=30°,∴∠DCE=∠FCE.在△DCE和△FCE中, 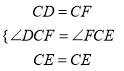 ,∴△DCE≌△FCE(SAS),∴DE=EF;
,∴△DCE≌△FCE(SAS),∴DE=EF;
(2)①∵△ABC是等腰直角三角形,∠ACB=90°,∴AC=BC,∠BAC=∠B=45°.∵∠DCF=90°,∴∠ACF=∠BCD.在△ACF和△BCD中, 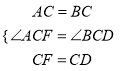 ,∴△ACF≌△BCD(SAS),∴∠CAF=∠B=45°,AF=DB,∴∠EAF=∠BAC+∠CAF=90°;
,∴△ACF≌△BCD(SAS),∴∠CAF=∠B=45°,AF=DB,∴∠EAF=∠BAC+∠CAF=90°;
②AE2+DB2=DE2,理由如下:
∵∠DCF=90°,∠DCE=45°,∴∠FCE=90°﹣45°=45°,∴∠DCE=∠FCE.在△DCE和△FCE中, 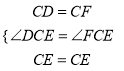 ,∴△DCE≌△FCE(SAS),∴DE=EF.在Rt△AEF中,AE2+AF2=EF2.又∵AF=DB,∴AE2+DB2=DE2.
,∴△DCE≌△FCE(SAS),∴DE=EF.在Rt△AEF中,AE2+AF2=EF2.又∵AF=DB,∴AE2+DB2=DE2.
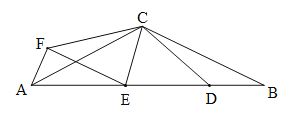
(3)【实际应用】把△BCD绕点C顺时针旋转120°得到△ACF,则△ACF≌△BCD.∵∠ACB=120°,AC=BC ,∴∠B=∠C=30°,∴∠CDE=∠B+∠BCD=30°+15°=45°,∴∠CDB=180°-45°=135°.∵△ACF≌△BCD,∴AE=DB,FC=DC,∠FCA=∠BCD=15°,∠FAC=∠B=30°,∠ACF=∠BDC=135°,∴∠FCE=∠ECD=60°.∵FC=DC,EC=EC,∴△FCE≌△DEC,∴EF=ED,∠CFE=∠CDE=45°,∴∠AFE=135°-45°=90°.∵∠FAE=30°+30°=60°,∴∠AEF=30°,∴AF:EF:AE=1: ![]() :2,∴S△BCD:S△DCE:S△ACE=BD:ED:AE= AF:EF:AE=1:
:2,∴S△BCD:S△DCE:S△ACE=BD:ED:AE= AF:EF:AE=1: ![]() :2.
:2.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,动点P按图中箭头所示方向从原点出发,第1次运动到P1(1,1),第2次接着运动到点P2(2,0),第3次接着运动到点P3(3,-2),…,按这的运动规律,点P2019的坐标是_____.
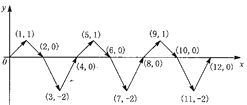
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,
,![]() 是
是![]() 的垂直平分线,点
的垂直平分线,点![]() 为垂足,
为垂足,![]() 的延长线与
的延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,连结
,连结![]() ,已知
,已知![]() ,
,![]() ,则图中长为4的线段有( )
,则图中长为4的线段有( )
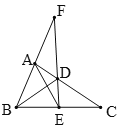
A. 5条B. 4条C. 3条D. 2条
查看答案和解析>>
科目:初中数学 来源: 题型:
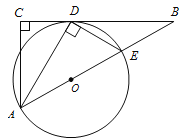
【题目】已知:如图,在△ABC 中,∠C=90°,∠BAC 的平分线 AD 交 BC于点 D,过点 D 作 DE⊥AD 交 AB 于点 E,以 AE 为直径作⊙O.
(1)求证:BC 是⊙O 的切线;
(2)若 AC=3,BC=4,求 BE 的长.
(3)在(2)的条件中,求 cos∠EAD 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
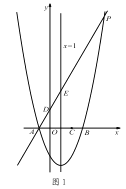
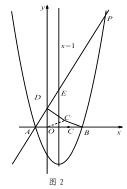
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
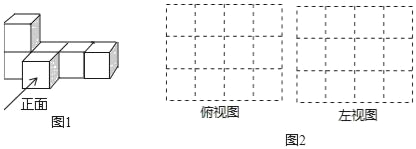
【题目】(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用2B铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天生产4500个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋 x个.
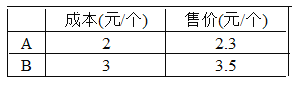
(1)用含x的整式表示每天的生产成本,并进行化简;
(2)用含x的整式表示每天获得的利润,并进行化简(利润=售价-成本);
(3)当x=1500时,求每天的生产成本与每天获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,射线AP交边BC于点E,点D是射线AP上一点,连接BD、CD .
(1)如图1,当∠CAB=45°,∠BDP=90°时,请直接写出DA与DB、DC之间满足的数量关系为: .
(2)如图2,当∠CAB=30°,∠BDP=60°时,试猜想:DA与DB、DC之间具有怎样的数量关系?并说明理由.
(3)如图3,当∠ACB=![]() ,∠BDP=
,∠BDP=![]() ,若
,若![]() 与
与![]() 之间满足
之间满足![]() ,则DA与DB、DC之间的数量关系为 .(请直接写出结论)
,则DA与DB、DC之间的数量关系为 .(请直接写出结论)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com