
【题目】在△ABC中,AC=BC,射线AP交边BC于点E,点D是射线AP上一点,连接BD、CD .
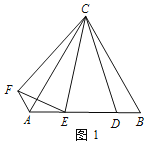
(1)如图1,当∠CAB=45°,∠BDP=90°时,请直接写出DA与DB、DC之间满足的数量关系为: .
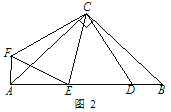
(2)如图2,当∠CAB=30°,∠BDP=60°时,试猜想:DA与DB、DC之间具有怎样的数量关系?并说明理由.
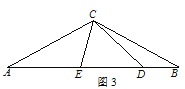
(3)如图3,当∠ACB=![]() ,∠BDP=
,∠BDP=![]() ,若
,若![]() 与
与![]() 之间满足
之间满足![]() ,则DA与DB、DC之间的数量关系为 .(请直接写出结论)
,则DA与DB、DC之间的数量关系为 .(请直接写出结论)

【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)AD=BD+CD·Sin
,证明见解析;(3)AD=BD+CD·Sin![]()
【解析】(1)结论:AD=BD+![]() CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,推出△CDM是等腰直角三角形,推出DM=
CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,推出△CDM是等腰直角三角形,推出DM=![]() CD,可得AD=AM+DM=BD+
CD,可得AD=AM+DM=BD+![]() CD;
CD;
(2)如图2中,结论∴AD=BD+![]() CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,作CH⊥DM于H,则MH=DH=CDcos30°=
CD.只要证明△ACM≌△BCD,推出CM=CD,AM=BD,作CH⊥DM于H,则MH=DH=CDcos30°=![]() CD,推出DM=
CD,推出DM=![]() CD,可得AD=AM+DM=BD+
CD,可得AD=AM+DM=BD+![]() CD;
CD;
(3)如图3中,结论:AD=BD+2CDcosα.证明方法类似.
(1)结论:AD=BD+![]() CD.
CD.
理由:如图1中,作CM⊥CD交AD于M.
∵∠ACE=∠BDE=90°,∠AEC=∠BED,
∴∠CAM=∠CBD,
∵∠ACB=∠MCD=90°,
∴∠ACM=∠BCD,
∵AC=CB,
∴△ACM≌△BCD,
∴CM=CD,AM=BD,
∴△CDM是等腰直角三角形,
∴DM=![]() CD,
CD,
∴AD=AM+DM=BD+![]() CD.
CD.
故答案为:AD=BD+![]() CD.
CD.
(2)如图2中,结论∴AD=BD+![]() CD.
CD.
理由:如图2中,作∠DCM=∠ACB交AD于M.
∵∠ACE=∠BDE=120°,∠AEC=∠BED,
∴∠CAM=∠CBD,
∵∠ACB=∠MCD,
∴∠ACM=∠BCD,
∵AC=CB,
∴△ACM≌△BCD,
∴CM=CD,AM=BD,
作CH⊥DM于H,则MH=DH=CDcos30°=![]() CD,
CD,
∴DM=![]() CD,
CD,
∴AD=AM+DM=BD+![]() CD;
CD;
(3)如图3中,结论:AD=BD+2CDcosα.
理由:如图3中,作∠DCM=∠ACB交AD于M.
∵∠ACE=∠BDE,∠AEC=∠BED,
∴∠CAM=∠CBD,
∵∠ACB=∠MCD,
∴∠ACM=∠BCD,
∵AC=CB,
∴△ACM≌△BCD,
∴CM=CD,AM=BD,
作CH⊥DM于H,则MH=DH=CDcosα,
∴DM=2CDcosα,
∴AD=AM+DM=BD+2CDcosα.
故答案为:AD=BD+2CDcosα.


科目:初中数学 来源: 题型:
【题目】【操作发现】如图 1,△ABC 为等边三角形,点 D 为 AB 边上的一点,∠DCE=30°,将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF,连接 AF、EF. 请直接 写出下列结果:
① ∠EAF的度数为__________;
② DE与EF之间的数量关系为__________;
【类比探究】如图 2,△ABC 为等腰直角三角形,∠ACB=90°,点 D 为 AB 边上的一点∠DCE=45°,将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF,连接 AF、EF.
①则∠EAF的度数为__________;
② 线段 AE,ED,DB 之间有什么数量关系?请说明理由;
【实际应用】如图 3,△ABC 是一个三角形的余料.小张同学量得∠ACB=120°,AC=BC, 他在边 BC 上取了 D、E 两点,并量得∠BCD=15°、∠DCE=60°,这样 CD、CE 将△
ABC 分成三个小三角形,请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况(超产记为正、减产记为负):

(1)写出该厂星期一生产工艺品的数量;
(2)本周产量最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
2, 4, 8, 16, 32, 64, …;①
0, 6, 6, 18, 30, 66, …;②
1, 2, 4, 8, 16, 32, …;③
(1)分别写出每一行的第![]() 个数;
个数;
(2)取每行数的第![]() 个数,使这三个数的和为162,求
个数,使这三个数的和为162,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,有理数![]() ,
,![]() ,
,![]() 在数轴上所对应的点分别是
在数轴上所对应的点分别是![]() ,
,![]() ,
,![]() 三点,且
三点,且![]() ,
,![]() ,
,![]() 满足;①
满足;①![]() ;②多项式
;②多项式![]() 是关于
是关于![]() 的二次三项式.
的二次三项式.
(1)![]() ,
,![]() ,
,![]() 的值分别是 (直接写出答案);
的值分别是 (直接写出答案);
(2)若数轴上点![]() ,
,![]() 之间有一动点
之间有一动点![]() ,且点
,且点![]() 对应的数为
对应的数为![]() ,化简
,化简![]() ;
;
(3)若点![]() 在数轴上以每秒1个单位的速度向左运动,同时点
在数轴上以每秒1个单位的速度向左运动,同时点![]() 和点
和点![]() 在数轴上分别以每秒
在数轴上分别以每秒![]() 个单位长度和4个单位长度的速度向右运动(其中
个单位长度和4个单位长度的速度向右运动(其中![]() ),若在整个运动过程中,点
),若在整个运动过程中,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离差始终不变,求运动几秒后点
的距离差始终不变,求运动几秒后点![]() 与点
与点![]() 的距离为13个单位长度.
的距离为13个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙两座仓库分别有农用车![]() 辆和
辆和![]() 辆,现需要调往
辆,现需要调往![]() 县
县![]() 辆, 调往
辆, 调往![]() 县
县![]() 辆,已知从甲仓库调运一辆农用车到
辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从乙仓库调运一辆农用车到
元,从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从甲仓库调往
元,从甲仓库调往![]() 县农用车
县农用车![]() 辆.
辆.
![]() 甲仓库调往
甲仓库调往![]() 县农用车____ 辆,乙仓库调往
县农用车____ 辆,乙仓库调往![]() 县农用车 _辆、乙仓库调往B县农用车____ 辆(用含
县农用车 _辆、乙仓库调往B县农用车____ 辆(用含![]() 的代数式表示);
的代数式表示);
![]() 写出公司从甲、乙两座仓库调农用车到
写出公司从甲、乙两座仓库调农用车到![]() 、
、![]() 两县所需要的总运费(用含
两县所需要的总运费(用含![]() 的代数式表示);
的代数式表示);
![]() 在
在![]() 的基础上,求当总运费是
的基础上,求当总运费是元时,从甲仓库调往
![]() 县农用车多少辆?
县农用车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
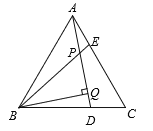
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
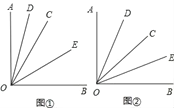
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出∠DOE的度数(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
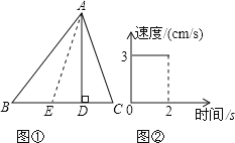
【题目】 如图①所示,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②所示,已知BC=8cm
(1)由图②,E点运动的时间为______s,速度为______cm/s
(2)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式;
(3)当E点停止后,求△ABE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com