
【题目】某公司在甲、乙两座仓库分别有农用车![]() 辆和
辆和![]() 辆,现需要调往
辆,现需要调往![]() 县
县![]() 辆, 调往
辆, 调往![]() 县
县![]() 辆,已知从甲仓库调运一辆农用车到
辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从乙仓库调运一辆农用车到
元,从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从甲仓库调往
元,从甲仓库调往![]() 县农用车
县农用车![]() 辆.
辆.
![]() 甲仓库调往
甲仓库调往![]() 县农用车____ 辆,乙仓库调往
县农用车____ 辆,乙仓库调往![]() 县农用车 _辆、乙仓库调往B县农用车____ 辆(用含
县农用车 _辆、乙仓库调往B县农用车____ 辆(用含![]() 的代数式表示);
的代数式表示);
![]() 写出公司从甲、乙两座仓库调农用车到
写出公司从甲、乙两座仓库调农用车到![]() 、
、![]() 两县所需要的总运费(用含
两县所需要的总运费(用含![]() 的代数式表示);
的代数式表示);
![]() 在
在![]() 的基础上,求当总运费是
的基础上,求当总运费是元时,从甲仓库调往
![]() 县农用车多少辆?
县农用车多少辆?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
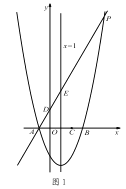
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
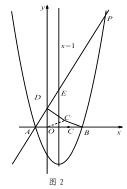
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB.
(2)如图2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积S= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,射线AP交边BC于点E,点D是射线AP上一点,连接BD、CD .
(1)如图1,当∠CAB=45°,∠BDP=90°时,请直接写出DA与DB、DC之间满足的数量关系为: .
(2)如图2,当∠CAB=30°,∠BDP=60°时,试猜想:DA与DB、DC之间具有怎样的数量关系?并说明理由.
(3)如图3,当∠ACB=![]() ,∠BDP=
,∠BDP=![]() ,若
,若![]() 与
与![]() 之间满足
之间满足![]() ,则DA与DB、DC之间的数量关系为 .(请直接写出结论)
,则DA与DB、DC之间的数量关系为 .(请直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期电影《少年的你》受到广大青少年的喜爱,某校七年级1班2班的几名同学请他们的家长在网上买票,家长了解到某电影院的活动,设购买电影票的张数为![]()
购买张数 |
|
|
|
每张票的价格 |
|
|
|
家长沟通后决定两个班的同学在期中考试结束后去观看。两个班共有![]() 人,期中
人,期中![]() 班人数多于
班人数多于![]() 不足
不足![]() 人。经过估算,如果两个班都以班为单位购买,则一共应付
人。经过估算,如果两个班都以班为单位购买,则一共应付![]() 元。
元。
![]() 求两个班有多少个同学?
求两个班有多少个同学?
![]() 如果两个班联合起来,作为一个团体购票,可以节省多少钱?
如果两个班联合起来,作为一个团体购票,可以节省多少钱?
![]() 如果七年级
如果七年级![]() 班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?
班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() 均是等边三角形,由这3个等边三角形组成一个新图形,现有下列结论:①
均是等边三角形,由这3个等边三角形组成一个新图形,现有下列结论:①![]() ;②
;②![]() 是一个平角;③
是一个平角;③![]() ;④新图形是一个轴对称图形,并且只有一条对称轴.其中正确的结论有( )
;④新图形是一个轴对称图形,并且只有一条对称轴.其中正确的结论有( )
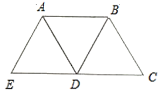
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在建设社会主义新农村过程中,某村委决定投资开发项目,现有6个项目可供选择,各项目所需资金及预计年利润如下表:
所需资金(亿元) | 1 | 2 | 4 | 6 | 7 | 8 |
预计利润(千万元) | 0.2 | 0.35 | 0.55 | 0.7 | 0.9 | 1 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计要获得0.9千万元的利润,你可以怎样投资项目?
(3)如果该村可以拿出10亿元进行多个项目的投资,预计最大年利润是多少?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com