
【题目】如图,![]() ,
,![]() ,
,![]() 均是等边三角形,由这3个等边三角形组成一个新图形,现有下列结论:①
均是等边三角形,由这3个等边三角形组成一个新图形,现有下列结论:①![]() ;②
;②![]() 是一个平角;③
是一个平角;③![]() ;④新图形是一个轴对称图形,并且只有一条对称轴.其中正确的结论有( )
;④新图形是一个轴对称图形,并且只有一条对称轴.其中正确的结论有( )
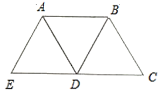
A.1个B.2个C.3个D.4个
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】观察下面三行数:
2, 4, 8, 16, 32, 64, …;①
0, 6, 6, 18, 30, 66, …;②
1, 2, 4, 8, 16, 32, …;③
(1)分别写出每一行的第![]() 个数;
个数;
(2)取每行数的第![]() 个数,使这三个数的和为162,求
个数,使这三个数的和为162,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙两座仓库分别有农用车![]() 辆和
辆和![]() 辆,现需要调往
辆,现需要调往![]() 县
县![]() 辆, 调往
辆, 调往![]() 县
县![]() 辆,已知从甲仓库调运一辆农用车到
辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从乙仓库调运一辆农用车到
元,从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为
县的运费分别为![]() 元和
元和![]() 元,从甲仓库调往
元,从甲仓库调往![]() 县农用车
县农用车![]() 辆.
辆.
![]() 甲仓库调往
甲仓库调往![]() 县农用车____ 辆,乙仓库调往
县农用车____ 辆,乙仓库调往![]() 县农用车 _辆、乙仓库调往B县农用车____ 辆(用含
县农用车 _辆、乙仓库调往B县农用车____ 辆(用含![]() 的代数式表示);
的代数式表示);
![]() 写出公司从甲、乙两座仓库调农用车到
写出公司从甲、乙两座仓库调农用车到![]() 、
、![]() 两县所需要的总运费(用含
两县所需要的总运费(用含![]() 的代数式表示);
的代数式表示);
![]() 在
在![]() 的基础上,求当总运费是
的基础上,求当总运费是元时,从甲仓库调往
![]() 县农用车多少辆?
县农用车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
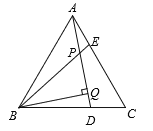
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象关于
的图象关于![]() 轴对称,
轴对称,![]() ,
,![]() 是函数
是函数![]() 图象上的两点,连接
图象上的两点,连接![]() ,点
,点![]() 是函数
是函数![]() 图象上的一点,连接
图象上的一点,连接![]() ,
,![]() .
.
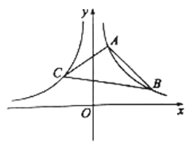
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 所在直线的表达式;
所在直线的表达式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
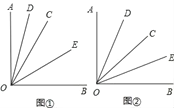
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出∠DOE的度数(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
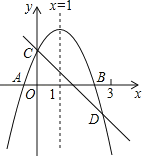
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com