
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
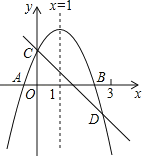
A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】利用抛物线与y轴的交点位置得到c>0,利用对称轴方程得到b=﹣2a,则2a+b+c=c>0,于是可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点在点(﹣1,0)右侧,则当x=﹣1时,y<0,于是可对②进行判断;根据二次函数的性质得到x=1时,二次函数有最大值,则ax2+bx+c≤a+b+c,于是可对③进行判断;由于直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,利用函数图象得x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,然后把b=﹣2a代入解a的不等式,则可对④进行判断.
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线的对称轴为直线x=﹣![]() =1,
=1,
∴b=﹣2a,
∴2a+b+c=2a﹣2a+c=c>0,所以①正确;
∵抛物线与x轴的一个交点在点(3,0)左侧,
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以②正确;
∵x=1时,二次函数有最大值,
∴ax2+bx+c≤a+b+c,
∴ax2+bx≤a+b,所以③正确;
∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,
∴x=3时,一次函数值比二次函数值大,
即9a+3b+c<﹣3+c,
而b=﹣2a,
∴9a﹣6a<﹣3,解得a<﹣1,所以④正确,
故选A.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() 均是等边三角形,由这3个等边三角形组成一个新图形,现有下列结论:①
均是等边三角形,由这3个等边三角形组成一个新图形,现有下列结论:①![]() ;②
;②![]() 是一个平角;③
是一个平角;③![]() ;④新图形是一个轴对称图形,并且只有一条对称轴.其中正确的结论有( )
;④新图形是一个轴对称图形,并且只有一条对称轴.其中正确的结论有( )
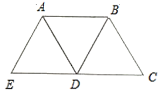
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以lcm/s的速度沿A→D→C方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是( )
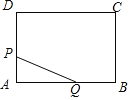
A.  B.
B. 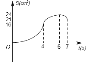 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在建设社会主义新农村过程中,某村委决定投资开发项目,现有6个项目可供选择,各项目所需资金及预计年利润如下表:
所需资金(亿元) | 1 | 2 | 4 | 6 | 7 | 8 |
预计利润(千万元) | 0.2 | 0.35 | 0.55 | 0.7 | 0.9 | 1 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计要获得0.9千万元的利润,你可以怎样投资项目?
(3)如果该村可以拿出10亿元进行多个项目的投资,预计最大年利润是多少?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
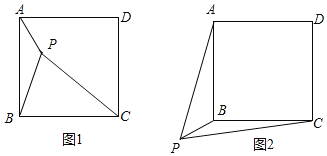
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
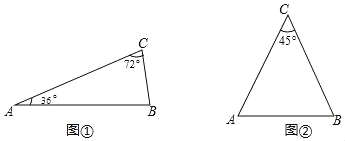
【题目】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
(1)如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
(2)如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
(应用)
(3)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的度数:___ ___ (写出其中两种情形即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司分两次采购甲、乙两种商品,具体情况如下:
商品 | 甲 | 乙 | 花费资金 |
次数 | |||
第一次采购件数 | 10件 | 15件 | 350元 |
第二次采购件数 | 15件 | 10件 | 375元 |
(1)求甲、乙商品每件各多少元?
(2)公司计划第三次采购甲、乙两种商品共31件,要求花费资金不超过475元,问最多可购买甲商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给下列证明过程填写理由.
如图,CD⊥AB于D,点F是BC上任意一点,EF⊥AB于E,∠1=∠2,求证:∠ACB=∠3.
请阅读下面解答过程,并补全所有内容.
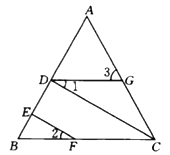
解:∵CD⊥AB,EF⊥AB(已知)
∴∠BEF=∠BDC=90°( )
∴EF∥DC( )
∴∠2=________( )
又∵∠2=∠1(已知)
∴∠1=_______(等量代换)
∴DG∥BC( )
∴∠3=________( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com