
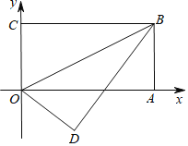
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,把矩形
,把矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,则点
处,则点![]() 的纵坐标为( )
的纵坐标为( )
A. -2B. -2.4C. -2![]() D. -2
D. -2![]()
【答案】B
【解析】
由折叠的性质得到一对角相等,再由矩形对边平行得到一对内错角相等,等量代换及等角对等边得到BE=OE,利用AAS得到三角形OED与三角形BEA全等,由全等三角形对应边相等得到DE=AE,过D作DF垂直于OE,利用勾股定理及面积法求出DF与OF的长,即可确定出D坐标.
解:由折叠得:∠CBO=∠DBO,
∵矩形ABCO,
∴BC∥OA,
∴∠CBO=∠BOA,
∴∠DBO=∠BOA,
∴BE=OE,
在△ODE和△BAE中,
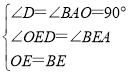 ,
,
∴△ODE≌△BAE(AAS),
∴AE=DE,
设DE=AE=x,则有OE=BE=8x,
在Rt△ODE中,根据勾股定理得:42+x2=(8x)2,
解得:x=3,即OE=5,DE=3,
过D作DF⊥OA,
∵S△OED=![]() ODDE=
ODDE=![]() OEDF,
OEDF,
∴DF=![]()
∴点![]() 的纵坐标为-
的纵坐标为-![]() =-2.4,
=-2.4,
故选B.


科目:初中数学 来源: 题型:
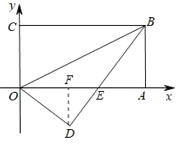
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表:
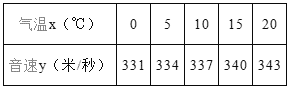
下列结论错误的是( )
A.在这个变化中,气温是自变量,音速是因变量
B.y随x的增大而增大
C.当气温为30°C时,音速为350米/秒
D.温度每升高5°C,音速增加3米/秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB:y=kx+b交y轴于点A(0,1),交x轴于点B(3,0).平行于y轴的直线x=1交AB于点D,交x轴于点E,点P是直线x=1上一动点,且在点D的上方,设P(1,n).
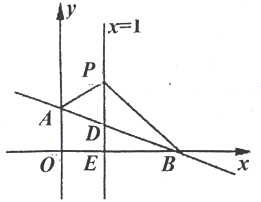
(1)求直线AB的表达式;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P为四边形ABCD内一点,且满足∠APB+∠CPD=180°, 则称点P为四边形ABCD的一个“互补点”.
(1)如图1,点P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.

(2)如图2,点P是菱形ABCD对角线上的任意一点.求证:点P为菱形ABCD的一个“互补点”.

查看答案和解析>>
科目:初中数学 来源: 题型:
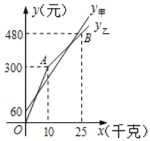
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与![]() 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与![]() 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,在乙园采摘草莓超过______![]() 后超过部分有打折优惠;
后超过部分有打折优惠;
(2)当采摘量![]() 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=![]() +bx+c图像的一部分,图像过点A(-3,0),对称轴是直线x=-1,给出四个结论,其中正确结论的个数为( )
+bx+c图像的一部分,图像过点A(-3,0),对称轴是直线x=-1,给出四个结论,其中正确结论的个数为( )

①c>0; ② 2a-b=0; ③![]() <0. ④若点B(-
<0. ④若点B(-![]() ,
,![]() )、C(-
)、C(-![]() ,
,![]() )在图像上,则
)在图像上,则![]() <
<![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
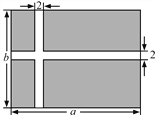
【题目】 某公园准备修建一块长方形草坪,长为a米,宽为b米.并在草坪上修建如图所示的十字路,
已知十字路宽2米.
(1)用含a、b的代数式表示修建的十字路的面积.
(2)若a=30,b=20,求草坪(阴影部分)的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com