
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
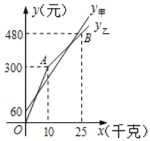
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与![]() 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与![]() 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,在乙园采摘草莓超过______![]() 后超过部分有打折优惠;
后超过部分有打折优惠;
(2)当采摘量![]() 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
【答案】(1)60,30;(2)20千克
【解析】
(1)根据函数图象和图象中的数据可以解答本题;
(2)根据函数图象中的数据可以求得当x>10时,y乙与x的函数表达式及 y甲与x的函数表达式,联立即可求解.
解:(1)由图象可得,
甲采摘园的门票是60元,两个采摘园优惠前的草莓单价是:300÷10=30(元/千克),
故答案为:60,30;
(2)当x>10时,设y乙与x的函数表达式是y乙=kx+b,
![]() ,得
,得![]() ,
,
即当x>10时,y乙与x的函数表达式是y乙=12x+180;
(3)由题意可得,
y甲=60+30×0.6x=18x+60,
当x>10时,令12x+180=18x+60,得x=20,
答:采摘20千克草莓时,甲、乙两家采摘园的总费用相同.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
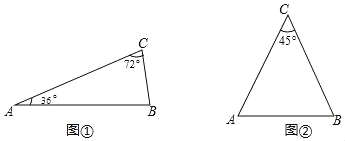
(1)如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
(2)如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
(应用)
(3)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的度数:___ ___ (写出其中两种情形即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 ![]() ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
ABC(如图1),按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是( )
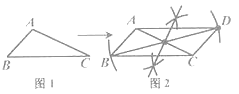
A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形 D. 对角线互相平分的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形,已知小长方形的长为a,宽为b,且a>b.
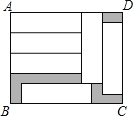
(1)用含a、b的代数式表示长方形ABCD的长AD、宽AB;
(2)用含a、b的代数式表示阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从M地出发沿一条公路匀速前往N地,乙骑摩托车从N地出发沿同一条公路匀速前往M地,
已知乙比甲晚出发0.5小时且先到达目的地.设甲行驶的时间为t(h),甲乙两人之间的路程为y(km),
y与t的函数关系如图1所示,请解决以下问题:
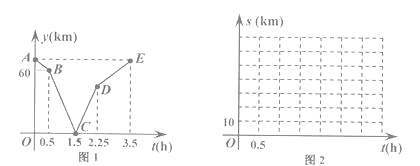
(1)写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式.
(2)①求点D的纵坐标.
②求M,N两地之间的距离.
(3)设乙离M地的路程为S乙 (km),请直接写出S甲 与时间t(h)的函数表达式,并在图2所给的直角坐标系中画出它的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
(实践操作)三角尺中的数学
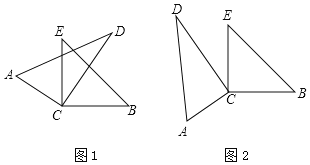
数学实践活动课上,“奋进”小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
(问题发现)
(1)①填空:如图1,若∠ACB=145°,则∠ACE的度数是 ,∠DCB的度数 ,∠ECD的度数是 .
②如图1,你发现∠ACE与∠DCB的大小有何关系?∠ACB与∠ECD的大小又有何关系?请直接写出你发现的结论.
(类比探究)
(2)如图2,当△ACD与△BCE没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知(x3+mx+n)(x2﹣3x+4)展开式中不含 x3和 x2项.
(1)求m、n的值;
(2)当 m、n取第(1)小题的值时,求(m+n)(m2﹣mn+n2)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com