
【题目】如图,在长方形ABCD中,放入6个形状和大小都相同的小长方形,已知小长方形的长为a,宽为b,且a>b.
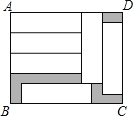
(1)用含a、b的代数式表示长方形ABCD的长AD、宽AB;
(2)用含a、b的代数式表示阴影部分的面积.
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
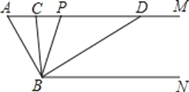
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB:y=kx+b交y轴于点A(0,1),交x轴于点B(3,0).平行于y轴的直线x=1交AB于点D,交x轴于点E,点P是直线x=1上一动点,且在点D的上方,设P(1,n).
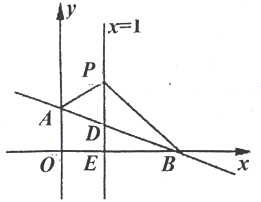
(1)求直线AB的表达式;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-3x与双曲线y=![]() 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向
上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与![]() 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与![]() 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,在乙园采摘草莓超过______![]() 后超过部分有打折优惠;
后超过部分有打折优惠;
(2)当采摘量![]() 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
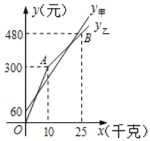
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
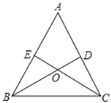
(1)上述三个条件中,由哪两个条件可以判定![]() 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某购物网店在双十一期间实行打折促销活动,规定如下表:
次性购物不大于100元不打折,不大于300元但大于100元打九折,超过300元的部分打八折.
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该网店一次性购物![]() 元,当
元,当![]() 低于300元但大于100元时,他实际付款多少元?当
低于300元但大于100元时,他实际付款多少元?当![]() 大于300元时,他实际付款多少元?(用含
大于300元时,他实际付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为![]() 元
元![]() ,用含
,用含![]() 的式子表示两次购物王老师实际付款多少元?
的式子表示两次购物王老师实际付款多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com