
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
科目:初中数学 来源: 题型:
【题目】如图,图①中△ABC是等边三角形,其边长是3,图②中△DEF是等腰直角三角形,∠F=90°,DF=EF=3.
(1)若S1为△ABC的面积,S2为△DEF的面积,S3=![]() AB·BC·sinB,S4=
AB·BC·sinB,S4=![]() DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
![]()
(2)在图③中,∠P=α(α为锐角),OP=m,PQ=n,△OPQ的面积为S,请你根据第(1)小题的解答,直接写出S与m,n以及α之间的关系式,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1的7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
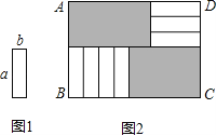
A. a=b B. a=2b
C. a=3b D. a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA’(点A落在直线l上点A’处、线段AP上的所有点与线段PA’上的点对应)如图1
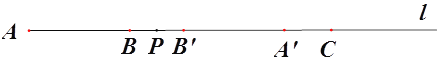
(1)若翻折后A’C=2,则翻折前线段AP= ;
(2)若点P在线段BC上运动,点M为线段A’C的中点,求线段PM的长度;
(3)若点P 在线段BC上运动,点N为B’P的中点,点M为线段A’C的中点,设AP=x,用x表示A’M+PN.

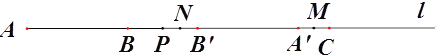
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
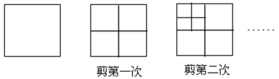
(1)完成下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的个数 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代数式表示)
.(用含n的代数式表示)
(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作a;设半圆O的半径为R,AM的长度为m,回答下列问题: 
(1)探究:若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是;如图2,当a=°时,半圆O与射线AB相切;
(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.
(3)发现:如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=(用含有R、m的代数式表示)
(4)拓展:如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是 , 并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com