
【题目】如图,直线l上依次有三点A、B、C,且AB=8、BC=16,点P为射线AB上一动点,将线段AP进行翻折得到线段PA’(点A落在直线l上点A’处、线段AP上的所有点与线段PA’上的点对应)如图1
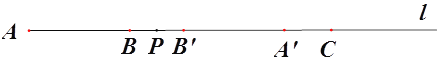
(1)若翻折后A’C=2,则翻折前线段AP= ;
(2)若点P在线段BC上运动,点M为线段A’C的中点,求线段PM的长度;
(3)若点P 在线段BC上运动,点N为B’P的中点,点M为线段A’C的中点,设AP=x,用x表示A’M+PN.

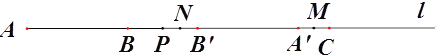
【答案】(1) 11 ;(2) PM=12 ;(3)  .
.
【解析】试题分析:
(1)如图1,由题意可知:AA′=AB+BC-A′C=22,由AP=A′P可得AP=11;
(2)如图3当点A′在点C的左侧时,由(1)可得此时AA′=22,结合已知易得此时:PM=PA′+A′M= ![]() =
= ![]() =
=![]() =12;如图4,当点A′在点C的右侧时,同理可得:PM=PA′-A′M=
=12;如图4,当点A′在点C的右侧时,同理可得:PM=PA′-A′M= ![]() =
=![]() =
= ![]() =12 ;由此即可得到PM=12;
=12 ;由此即可得到PM=12;
(3)根据题意分:①当8<x<12;②当x>12两种情况结合图5、图6分析解答即可.
试题解析:
(1)如图1,当翻折后点A′在点C的左侧时,∵AB=8,BC=16,A′C=2,
∴AA′=AB+BC-A′C=22,
又∵由折叠的性质可知:AP=A′P,
∴AP=11;

(2)①当A′在点C的左侧时,如图3,

由题知PA=PA′,
∵M为AC中点,
∴MA′=MC,
∴PM=PA′+A′M= ![]() =
= ![]() =
=![]() =12;
=12;
②当A′在点C的右侧时,如图4,

∵M为A′C中点,
∴MA′=MC,
∴PM=PA′-A′M= ![]() =
=![]() =
= ![]() =12 ;
=12 ;
综上可得:PM=12 ;
(3)①当8<x<12 此时,A′在C的左侧,如图5,

PB′=PB=x-8,
∵N为BP中点,
∴![]() ,
,
∵A′C=24-2x,
∵M为A′C中点,
∴![]() ,
,
∴![]()
![]() ;
;
②当x>12 ,此时,A′在C的右侧,如图6
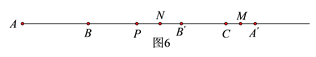
PB′=PB=x-8, ![]() ,
,
A′C=2x-24,
∵M为A′C中点,
∴![]() ,
,
∴![]()
![]() ;
;
③当x>24时,如图7,点P不在线段BC上了,不予考虑,
![]()
∴综上所述: 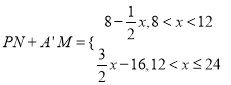 .
.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E. 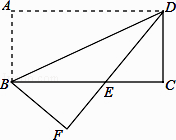
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)x2y﹣3xy2+2x2y﹣y2x ;(2)2(2a2﹣9b)﹣3(3a2﹣7b);
(3)2a2﹣[![]() (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣![]() ab.
ab.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船,该艘货船以每小时10海里的速度向正东航行,海警船立即以每小时14海里的速度追赶,到C处相遇,求海警船用多长时间追上了货船?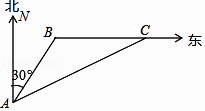
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1与直线y=﹣ax+c相交于坐标轴上点A(﹣3,0),C(0,1)两点.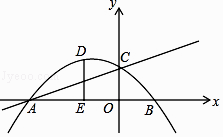
(1)直线的表达式为;抛物线的表达式为 .
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交直线AC于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)P为抛物线上一动点,且P在第四象限内,过点P作PN垂直x轴于点N,使得以P、A、N为顶点的三角形与△ACO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,为加强生态城市建设,邢台市大力发展绿色交通,构建公共、绿色交通体系,2016年11月28日公共自行车陆续放置在车桩中,琪琪随机调查了若干市民租用公共自行车的骑车时间:(单位:h),将获得的数据分成五组,绘制了如下统计图,请根据图中信息,解答下列问题. 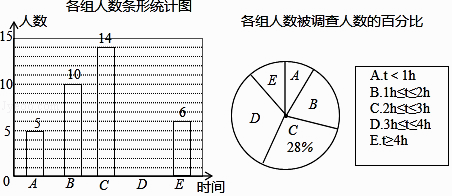
(1)这次被调查的总人数是多少?
(2)试求表示D组的扇形圆心角的度数,并补全条形统计图;
(3)公共自行车系统投入使用后,按规定市民借车1小时内免费,1小时至2小时收费1元,2小时至3小时收费3元,3小时以上,在3元的基础上,每小时加收3元(不足1小时均按1小时计算)请估算,在租用公共自行车的市民中,缴费超过3元的人数所占的百分比.
(4)A组5人中3女2男,从中随机抽取2人,则恰好是一男一女的为事件A,用列表法或者树状图法求出事件A的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的5×5网格中,小方格的边长为1.
(1)图中格点正方形ABCD的面积为________;
(2)若连接AC,则以AC为边的正方形的面积为________;
(3)在所给网格中画一个格点正方形,使其各边都不在格线上且面积最大,你所画的正方形面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com