练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    （1）x2y﹣3xy2+2x2y﹣y2x ；（2）2（2a2﹣9b）﹣3（3a2﹣7b）；

    （3）2a2﹣[（ab﹣4a2）+8ab]﹣ab.

    【答案】（1）3x2y﹣4xy2；（2）－5a2+3b；（3）4a2﹣9ab.

    【解析】

    （1）（2）根据整式的加减运算顺序，没有括号，直接合并同类项即可，合并同类项时，只把系数相加减，字母与字母的指数不变．

    （3）去括号后合并同类项即可．

    （1）原式=（x2y+2 x2y）+（﹣3xy2﹣y2x）=3x2y﹣4xy2；

    （2）原式=4a2﹣18b﹣9a2+21b

    =（4a2﹣9a2）+（21b﹣18b）

    =﹣5a2+3b

    （3）原式=2a2﹣[﹣2a2+ab]﹣ab

    =2a2+2a2﹣ab﹣ab

    =4a2﹣9ab．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】观察下列等式的规律，解答下列问题：

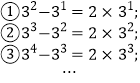
    （1）按此规律，第④个等式为_________；第个等式为_______；（用含的代数式表示，为正整数）

    （2）按此规律，计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．

    （1）求证：△AEH∽△ABC；

    （2）求这个正方形的边长与面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“十一”国庆期间出租车司机小李某天下午的营运始终在长安街（自东向西或自西向东）上进行，如果规定向东为正，向西为负，他这天下午从天安门出发，行车里程（单位：千米）如下：

    +15，﹣2，+5，﹣1，+10，﹣3，﹣2，+12，+4，﹣5，+6．

    （1）小李将最后一名乘客送抵目的地时，小李距天安门有多远？

    （2）如果汽车耗油量为0.08升/千米，这天下午小李共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

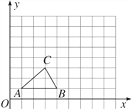
    【题目】如图，在9×9网格中，每个小方格的边长看作单位1，每个小方格的顶点叫作格点，△ABC的顶点都在格点上．

    (1)请在网格中画出△ABC的一个位似图形△A1B1C，使两个图形以点C为位似中心，且所画图形与△ABC的相似比为2∶1；

    (2)将△A1B1C绕着点C顺时针旋转90°得△A2B2C，画出图形，并在如图所示的坐标系中分别写出△A2B2C三个顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1的7张长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）

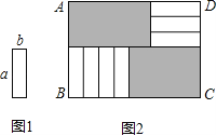
    A. a=b B. a=2b

    C. a=3b D. a=4b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中A（0，0），B（2，0），△AP1B是等腰直角三角形，且∠P1=90°，把△AP1B绕点B顺时针旋转180°，得到△BP2C；把△BP2C绕点C顺时针旋转180°，得到△CP3D，依此类推，则旋转第2016次后，得到的等腰直角三角形的直角顶点P2017的坐标为（ ）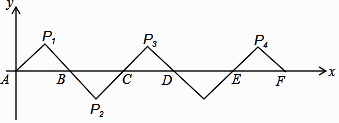

    A.（4030，1）
    B.（4029，﹣1）
    C.（4033，1）
    D.（4031，﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l上依次有三点A、B、C，且AB=8、BC=16，点P为射线AB上一动点，将线段AP进行翻折得到线段PA’（点A落在直线l上点A’处、线段AP上的所有点与线段PA’上的点对应）如图1

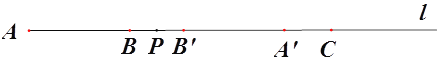
    （1）若翻折后A’C=2，则翻折前线段AP= ；

    （2）若点P在线段BC上运动，点M为线段A’C的中点，求线段PM的长度；

    （3）若点P 在线段BC上运动，点N为B’P的中点，点M为线段A’C的中点，设AP=x，用x表示A’M+PN.

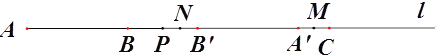
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据题意解答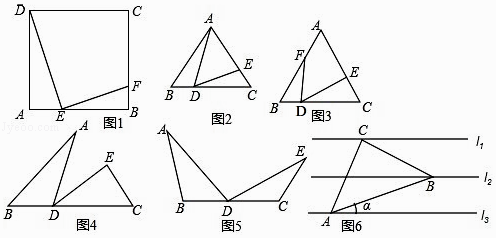

    （1）如图1，已知E是矩形ABCD的边AB上一点，EF⊥DE交BC于点F，证明：△ADE∽△BFE．
    （2）这个相似的基本图形像字母K，可以称为“K”型相似，但更因为图形的结构特征是一条线上有3个垂直关系，也常被称为“一线三垂直”，那普通的3个等角又会怎样呢？
    变式一如图2，已知等边三角形ABC，点D、E分别为BC，AC上的点，∠ADE=60°．
    ①图中有相似三角形吗？请说明理由．
    ②如图3，若将∠ADE在△ABC的内部（∠ADE两边不与BC重合），绕点D逆时针旋转一定的角度，还有相似三角形吗？
    （3）变式二如图4，隐藏变式1图形中的线段AE，在得到的新图形中．
    ①如果∠B=∠C=∠ADE=50°，图中有相似三角形吗？请说明理由．
    ②如图5，若∠B=∠C=∠ADE=∠a，∠a为任意角，还有相似三角形吗？
    （4）交式三已知，相邻两条平形直线间的距离相等，若等腰直角△ABC的三个顶点分别在这三条平行直线上，则cosa的值是（直接写出结果）．

    查看答案和解析>>

    同步练习册答案